
【題目】已知圓![]() 上一動點
上一動點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() 點,
點,![]() 中點為
中點為![]() .
.
(1)當![]() 在圓
在圓![]() 上運動時,求點
上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求線段
時,求線段![]() 的垂直平分線方程.
的垂直平分線方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】分析:(1)要求點![]() 的軌跡
的軌跡![]() 的方程,可設點
的方程,可設點![]() 的坐標為
的坐標為![]() ,由條件過點
,由條件過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() 點,
點,![]() 中點為
中點為![]() ,可寫出點A的坐標
,可寫出點A的坐標![]() 。因為點
。因為點![]() 在圓
在圓![]() 上,故可將點
上,故可將點![]() 的坐標代入圓
的坐標代入圓![]() 的方程
的方程![]() ,可得點
,可得點![]() 的軌跡
的軌跡![]() 。
。
(2)要線段![]() 的垂直平分線方程,應先求直線
的垂直平分線方程,應先求直線![]() 的方程,所以應設直線
的方程,所以應設直線![]() 的方程,根據弦長求直線
的方程,根據弦長求直線![]() 的方程。因為直線
的方程。因為直線![]() 的斜率是否存在不確定,為了避免討論,可設直線
的斜率是否存在不確定,為了避免討論,可設直線![]() 方程為:
方程為:![]() ,并與軌跡
,并與軌跡![]() 的方程聯立可得
的方程聯立可得![]() ,由根與系數的關系可得
,由根與系數的關系可得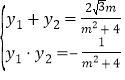 ,由弦長公式可得
,由弦長公式可得![]() ,可解得
,可解得![]() 。分情況討論,求線段
。分情況討論,求線段![]() 的中點,直線
的中點,直線![]() 的斜率,進而可求線段
的斜率,進而可求線段![]() 的垂直平分線方程。
的垂直平分線方程。
詳解:(1)設![]() ,則
,則![]()
將![]() 代入圓
代入圓![]() 方程得:點
方程得:點![]() 的軌跡
的軌跡![]()
(注:學生不寫![]() 也不扣分)
也不扣分)
(2)由題意可設直線![]() 方程為:
方程為:![]() ,
,
由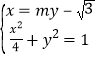 得:
得:![]()
所以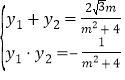
![]()
所以![]() .
.
當![]() 時,中點縱坐標
時,中點縱坐標![]() ,代入
,代入![]() 得:
得:
中點橫坐標![]() ,斜率為
,斜率為![]()
故![]() 的垂直平分線方程為:
的垂直平分線方程為:![]()
當![]() 時,同理可得
時,同理可得![]() 的垂直平分線方程為:
的垂直平分線方程為:![]()
所以![]() 的垂直平分線方程為:
的垂直平分線方程為:![]() 或
或![]() .
.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,在區間
,在區間![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,設函數
,設函數![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)方程![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示,求數學成績在[50,90)之外的人數.
分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在考察黃煙經過藥物處理和發生青花病的關系時,得到如下數據:在試驗的470株黃煙中,經過藥物處理的黃煙有25株發生青花病,60株沒有發生青花病;未經過藥物處理的有185株發生青花病,200株沒有發生青花病.試推斷藥物處理跟發生青花病是否有關系.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某技校開展技能大賽,甲、乙兩班各選取5名學生加工某種零件,在4個小時內每名學生加工的合格零件數的統計數據的莖葉圖如圖所示,已知甲班學生在4個小時內加工的合格零件數的平均數為21,乙班學生在4個小時內加工的合格零件數的平均數不低于甲班的平均數.
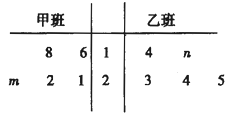
(1)求![]() 的值;
的值;
(2)分別求出甲、乙兩班學生在4個小時內加工的合格零件數的方差![]() 和
和![]() ,并由此比較兩班學生的加工水平的穩定性.
,并由此比較兩班學生的加工水平的穩定性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.在購進機器時,可以一次性額外購買幾次維修服務,每次維修服務費用200元,另外實際維修一次還需向維修人員支付小費,小費每次50元.在機器使用期間,如果維修次數超過購機時購買的維修服務次數,則每維修一次需支付維修服務費用500元,無需支付小費.現需決策在購買機器時應同時一次性購買幾次維修服務,為此搜集并整理了100臺這種機器在三年使用期內的維修次數,得下面統計表:
維修次數 | 8 | 9 | 10 | 11 | 12 |
頻數 | 10 | 20 | 30 | 30 | 10 |
記x表示1臺機器在三年使用期內的維修次數,y表示1臺機器在維修上所需的費用(單位:元),![]() 表示購機的同時購買的維修服務次數.
表示購機的同時購買的維修服務次數.
(1)若![]() =10,求y與x的函數解析式;
=10,求y與x的函數解析式;
(2)若要求“維修次數不大于![]() ”的頻率不小于0.8,求n的最小值;
”的頻率不小于0.8,求n的最小值;
(3)假設這100臺機器在購機的同時每臺都購買10次維修服務,或每臺都購買11次維修服務,分別計算這100臺機器在維修上所需費用的平均數,以此作為決策依據,購買1臺機器的同時應購買10次還是11次維修服務?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com