
【題目】為支援武漢抗擊疫情,某醫院準備從6名醫生和3名護士中選出5人組成一個醫療小組遠赴武漢,請解答下列問題:(用數字作答)
(1)如果這個醫療小組中醫生和護士都不能少于2人,共有多少種不同的建組方案?
(2)醫生甲要擔任醫療小組組長,所以必選,而且醫療小組必須醫生和護士都有,共有多少種不同的建組方案?
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】上海市復興高級中學二期改擴建工程于2015年9月正式開始,現需要圍建一個面積火900平方米的矩形地場地的圍墻,有一面長度為20米的舊墻(圖中斜杠部),有甲、乙兩種維修利用舊墻方案.

甲方案:選取部分舊墻(選取的舊墻的長度設為![]() 米,
米,![]() ),維修后單獨作為矩形場地的一面圍墻(如方案①圖),多余部分不維修;
),維修后單獨作為矩形場地的一面圍墻(如方案①圖),多余部分不維修;
乙方案:舊墻全部利用維修后,再續建一段新墻(新墻的長度高![]() 米),共同作為矩形場地的一面(如方案②圖)
米),共同作為矩形場地的一面(如方案②圖)
已知舊墻維修費用為10元/米,新墻造價為80元/米,設修建總費用![]() .
.
(1)如果按甲方案修建,試用解析式將修建總費用![]() 表示成關于
表示成關于![]() 的函數;
的函數;
(2)如果按乙方案修建,試用解析式將修建總費用![]() 表示成關于
表示成關于![]() 的函數;
的函數;
(3)試求出兩種方案中修建總費用![]() ,
,![]() 的最小值,并比較哪種方案最節省費用?
的最小值,并比較哪種方案最節省費用?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩條直線l1:y=m 和l2:y![]() (m>0),直線l1與函數y=|log2x|的圖象從左至右相交于點A,B,直線l2與函數y=|log2x|的圖象從左至右相交于C,D.記線段AC和BD在X軸上的投影長度分別為a 和b.當m變化時,
(m>0),直線l1與函數y=|log2x|的圖象從左至右相交于點A,B,直線l2與函數y=|log2x|的圖象從左至右相交于C,D.記線段AC和BD在X軸上的投影長度分別為a 和b.當m變化時,![]() 的最小值為()
的最小值為()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+e-x,g(x)=2x+ax3,a為實常數.
(1)求g(x)的單調區間;
(2)當a=-1時,證明:存在x0∈(0,1),使得y=f(x)和y=g(x)的圖象在x=x0處的切線互相平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,質量測試分為:指標不小于90為一等品,不小于80小于90為二等品,小于80為三等品,每件一等品盈利50元,每件二等品盈利30元,每件三等品虧損10元,現對學徒工甲和正式工人乙生產的產品各100件的檢測結果統計如下:
測試指標 |
|
|
|
|
|
|
甲 | 5 | 15 | 35 | 35 | 7 | 3 |
乙 | 3 | 7 | 20 | 40 | 20 | 10 |
根據上表統計得到甲、乙生產產品等級的頻率分別估計為他們生產產品等級的概率.
(1)求出乙生產三等品的概率;
(2)求出甲生產一件產品,盈利不小于30元的概率;
(3)若甲、乙一天生產產品分別為40件和30件,估計甲、乙兩人一天共為企業創收多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A市積極倡導學生參與綠色環保活動,其中代號為“環保衛士——12369”的綠色環保活動小組對2014年1月——2014年12月(一年)內空氣質量指數![]() 進行監測,下表是在這一年隨機抽取的100天的統計結果:
進行監測,下表是在這一年隨機抽取的100天的統計結果:
指數API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空氣質量 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中重度污染 | 重度污染 |
天數 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若A市某企業每天由空氣污染造成的經濟損失P(單位:元)與空氣質量指數![]() (記為t)的關系
(記為t)的關系
為: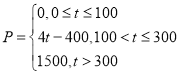 ,在這一年內隨機抽取一天,估計該天經濟損失
,在這一年內隨機抽取一天,估計該天經濟損失![]() 元的概率;
元的概率;
(2)若本次抽取的樣本數據有30天是在供暖季節,其中有8天為重度污染,完成![]() 列聯表,并判斷是
列聯表,并判斷是
否有![]() 的把握認為A市本年度空氣重度污染與供暖有關?
的把握認為A市本年度空氣重度污染與供暖有關?
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季節 | |||
合計 | 100 |
下面臨界值表供參考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | p>5.024 | 6.635 | 7.879 | 10.828 |
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】非空集合![]() 關于運算
關于運算![]() 滿足:①對任意
滿足:①對任意![]() ,都有
,都有![]() ;②存在
;②存在![]() 使得對于一切
使得對于一切![]() 都有
都有![]() ,則稱
,則稱![]() 是關于運算
是關于運算![]() 的融洽集,現有下列集合與運算:①
的融洽集,現有下列集合與運算:①![]() 是非負整數集,
是非負整數集,![]() :實數的加法;②
:實數的加法;②![]() 是偶數集,
是偶數集,![]() :實數的乘法;③
:實數的乘法;③![]() 是所有二次三項式構成的集合,
是所有二次三項式構成的集合,![]() :多項式的乘法; ④
:多項式的乘法; ④![]() ,
,![]() :實數的乘法;其中屬于融洽集的是________(請填寫編號)
:實數的乘法;其中屬于融洽集的是________(請填寫編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐A﹣BCD中,AB=AD,BD⊥CD,點E、F分別是棱BC、BD的中點.
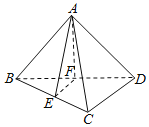
(1)求證:EF∥平面ACD;
(2)求證:AE⊥BD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com