
【題目】如圖,在三棱錐A﹣BCD中,AB=AD,BD⊥CD,點E、F分別是棱BC、BD的中點.
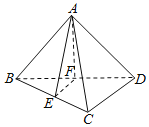
(1)求證:EF∥平面ACD;
(2)求證:AE⊥BD.
 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源: 題型:
【題目】為支援武漢抗擊疫情,某醫院準備從6名醫生和3名護士中選出5人組成一個醫療小組遠赴武漢,請解答下列問題:(用數字作答)
(1)如果這個醫療小組中醫生和護士都不能少于2人,共有多少種不同的建組方案?
(2)醫生甲要擔任醫療小組組長,所以必選,而且醫療小組必須醫生和護士都有,共有多少種不同的建組方案?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩隊參加聽歌猜歌名游戲,每隊![]() 人.隨機播放一首歌曲, 參賽者開始搶答,每人只有一次搶答機會,答對者為本隊贏得一分,答錯得零分, 假設甲隊中每人答對的概率均為
人.隨機播放一首歌曲, 參賽者開始搶答,每人只有一次搶答機會,答對者為本隊贏得一分,答錯得零分, 假設甲隊中每人答對的概率均為![]() ,乙隊中
,乙隊中![]() 人答對的概率分別為
人答對的概率分別為![]() ,且各人回答正確與否相互之間沒有影響.
,且各人回答正確與否相互之間沒有影響.
(1)若比賽前隨機從兩隊的![]() 個選手中抽取兩名選手進行示范,求抽到的兩名選手在同一個隊的概率;
個選手中抽取兩名選手進行示范,求抽到的兩名選手在同一個隊的概率;
(2)用![]() 表示甲隊的總得分,求隨機變量
表示甲隊的總得分,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(3)求兩隊得分之和大于4的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直三棱柱![]() ,其中P為棱
,其中P為棱![]() 上的任意一點,設平面PAB與平面
上的任意一點,設平面PAB與平面![]() 的交線為QR.
的交線為QR.

(1)求證:AB∥QR;
(2)若P為棱![]() 上的中點,求幾何體
上的中點,求幾何體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
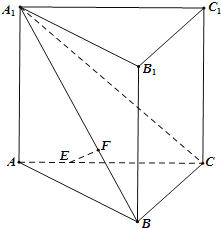
【題目】如圖,在直三棱柱![]() 側棱和底面垂直的棱柱
側棱和底面垂直的棱柱![]() 中,平面
中,平面![]() 側面
側面![]() ,
,![]() ,線段AC、
,線段AC、![]() 上分別有一點E、F且滿足
上分別有一點E、F且滿足![]() ,
,![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 求點E到直線
求點E到直線![]() 的距離;
的距離;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為支援邊遠地區教育事業的發展,現有5名師范大學畢業生主動要求赴西部某地區三所不同的學校去支教,每個學校至少去1人,甲、乙不能安排在同一所學校,則不同的安排方法有( )
A.180種B.150種C.90種D.114種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,過橢圓的左、右焦點
,過橢圓的左、右焦點![]() 分別作傾斜角為
分別作傾斜角為![]() 的直線
的直線![]() ,
,![]() 分別交橢圓于A,B和C,D兩點,當
分別交橢圓于A,B和C,D兩點,當![]() 時,直線AB與CD之間的距離為
時,直線AB與CD之間的距離為![]() .
.
(1)求橢圓的標準方程;
(2)若AB不與x軸重合,點P在橢圓上,且滿足![]() (t>0).若
(t>0).若![]() ,求直線AB的方程.
,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 上頂點為A,右頂點為B,離心率
上頂點為A,右頂點為B,離心率![]() ,O為坐標原點,原點到直線AB的距離為
,O為坐標原點,原點到直線AB的距離為![]() .
.
(1)求橢圓C的標準方程;
(2)直線![]() 與橢圓C相交于E、F兩不同點,若橢圓C上一點P滿足
與橢圓C相交于E、F兩不同點,若橢圓C上一點P滿足![]() .求△EPF面積的最大值及此時的
.求△EPF面積的最大值及此時的![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com