
分析 (1)由題意設出橢圓方程,再由拋物線方程求出拋物線焦點坐標,可得橢圓的短半軸長,結合離心率及隱含條件求得a,則橢圓方程可求;
(2)由題意可設直線l的方程為y=k(x-2)+1 (k≠0),聯立直線方程和橢圓方程,由判別式等于0求得k,進一步求得切點M的坐標;
(3)若存在直線l1滿足條件,則直線l1的斜率存在,設其方程為y=k1(x-2)+1,聯立直線方程和橢圓方程,化為關于x的一元二次方程,利用根與系數的關系求出A,B的橫坐標的和與積,結合向量等式求得k1得答案.
解答 解:(1)設橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 (a>b>0),
由拋物線x2=-4$\sqrt{3}$y,得拋物線焦點F(0,-$\sqrt{3}$),
由題意得b=$\sqrt{3}$,$\frac{c}{a}$=$\frac{1}{2}$,解得a=2,c=1.
故橢圓C的標準方程為$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)∵過點P(2,1)的直線l與橢圓C在第一象限相切,∴直線l的斜率存在,
故可設直線l的方程為y=k(x-2)+1 (k≠0).
由 $\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x-2)+1}\end{array}\right.$
得(3+4k2)x2-8k(2k-1 )x+16k2-16k-8=0.①
∵直線l與橢圓C相切,
∴△=[-8k(2k-1)]2-4(3+4k2)(16k2-16k-8)=0.
整理,得32(6k+3)=0,解得k=-$\frac{1}{2}$.
∴直線l的方程為y=-$\frac{1}{2}$(x-2)+1=-$\frac{1}{2}$x+2.
將k=-$\frac{1}{2}$代入①式,解得M點的橫坐標為1,故切點M的坐標為;
(3)若存在直線l1滿足條件,則直線l1的斜率存在,設其方程為y=k1(x-2)+1,
代入橢圓C的方程得:(3+4k)x2-8k1(2k1-1)x+16k-16k1 -8=0.
設A(x1,y1),B(x2,y2),
∵直線l1與橢圓C相交于不同的兩點A,B,
∴△=[-8k1(2k1-1)]2-4(3+4k)(16k-16k1-8)=32(6k1+3)>0,得k1>-$\frac{1}{2}$.
x1+x2=$\frac{8{k}_{1}(2{k}_{1}-1)}{3+4{{k}_{1}}^{2}}$,x1x2=$\frac{16{{k}_{1}}^{2}-16{k}_{1}-8}{3+4{{k}_{1}}^{2}}$.
∵$\overrightarrow{PA}•\overrightarrow{PB}={\overrightarrow{PM}}^{2}$,即(x1-2)(x2-2)+(y1-1)(y2-1)=$\frac{5}{4}$,
∴(x1-2)(x2-2)(1+k)=$\frac{5}{4}$,即[x1x2-2(x1+x2)+4](1+k)=$\frac{5}{4}$,
∴[$\frac{8{k}_{1}(2{k}_{1}-1)}{3+4{{k}_{1}}^{2}}$-2$\frac{16{{k}_{1}}^{2}-16{k}_{1}-8}{3+4{{k}_{1}}^{2}}$+4](1+k)═$\frac{4+4{{k}_{1}}^{2}}{3+4{{k}_{1}}^{2}}$=$\frac{5}{4}$,
解得k1=±$\frac{1}{2}$.
∵A,B為不同的兩點,∴k1=$\frac{1}{2}$.
于是存在直線l1滿足條件,其方程為y=$\frac{1}{2}$x.
點評 本題考查橢圓的簡單性質,考查了直線與橢圓位置關系的應用,體現了“設而不求”的解題思想方法,是中檔題.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | $5+\sqrt{2}$ | C. | $4+\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 重合 | B. | 形狀相同,位置不同 | ||
| C. | 關于y軸對稱 | D. | 形狀不同,位置不同 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在如圖所示的多面體中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=4,EF=3,AD=AE=BE=2,G是BC的中點.
在如圖所示的多面體中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=4,EF=3,AD=AE=BE=2,G是BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
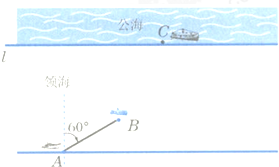 設直線l為公海的分界線,一巡邏艇在A處發現了北偏東60°的海面B處有一艘走私船,走私船正向停泊在公海上接應的走私海輪C航行,以便上海輪后逃竄.已知巡邏艇的航速是走私船航速的2倍,A與公海相距約為20海里,走私船可能向任一方向逃竄,請回答下列問題:
設直線l為公海的分界線,一巡邏艇在A處發現了北偏東60°的海面B處有一艘走私船,走私船正向停泊在公海上接應的走私海輪C航行,以便上海輪后逃竄.已知巡邏艇的航速是走私船航速的2倍,A與公海相距約為20海里,走私船可能向任一方向逃竄,請回答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com