
分析 由$[\begin{array}{l}{a}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}k\\-1\end{array}]$=λ$[\begin{array}{l}k\\-1\end{array}]$,即$\left\{\begin{array}{l}{ak-k=kλ}\\{-1=-λ}\end{array}\right.$,由k≠0,解得:$\left\{\begin{array}{l}{λ=1}\\{a=2}\end{array}\right.$,根據矩陣的運算性質可知:A$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,$[\begin{array}{l}{2}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,即可求得k的值,求得a+k的值.
解答 解:設特征向量為$\overrightarrow{a}$=$[\begin{array}{l}k\\-1\end{array}]$,對應的特征值為λ,λ,
則$[\begin{array}{l}{a}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}k\\-1\end{array}]$=λ$[\begin{array}{l}k\\-1\end{array}]$,即$\left\{\begin{array}{l}{ak-k=kλ}\\{-1=-λ}\end{array}\right.$,
由k≠0,解得:$\left\{\begin{array}{l}{λ=1}\\{a=2}\end{array}\right.$,
由A-1$[\begin{array}{l}{3}\\{1}\end{array}]$=$[\begin{array}{l}{1}\\{1}\end{array}]$,即A$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,
$[\begin{array}{l}{2}&{k}\\{0}&{1}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=$[\begin{array}{l}{3}\\{1}\end{array}]$,即$\left\{\begin{array}{l}{2+k=3}\\{1=1}\end{array}\right.$,解得:k=1,
∴a+k=2+1=3,
故答案為:3.
點評 本題考查矩陣的運算,考查矩陣的特征值與特征向量的計算,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
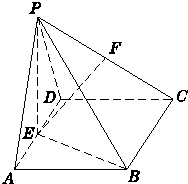 如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,△PAD是等邊三角形,底面ABCD是邊長為2的菱形,∠BAD=60°,E是AD的中點,F是PC的中點.
如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,△PAD是等邊三角形,底面ABCD是邊長為2的菱形,∠BAD=60°,E是AD的中點,F是PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com