
分析 根據函數的奇偶性作出函數f(x)的圖象,利用換元法判斷函數t=f(x)的根的個數,利用數形結合即可得到結論.
解答 解:作出函數f(x)的圖象如圖:
則f(x)在(-∞,-2)和(0,2)上遞增,在(-2,0)和(2,+∞)上遞減,
當x=±2時,函數取得極大值f(2)=$\frac{5}{4}$;
當x=0時,取得極小值0.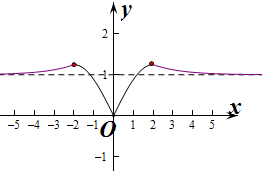
要使關于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且只有6個不同實數根,
設t=f(x),則當t<0,方程t=f(x),有0個根,
當t=0,方程t=f(x),有1個根,
當0<t≤1或t=$\frac{5}{4}$,方程t=f(x),有2個根,
當1<t<$\frac{5}{4}$,方程t=f(x),有4個根,
當t>$\frac{5}{4}$,方程t=f(x),有0個根.
則t2+at+b=0必有兩個根t1、t2,
則有兩種情況符合題意:
①t1=$\frac{5}{4}$,且t2∈(1,$\frac{5}{4}$),
此時-a=t1+t2,
則a∈(-$\frac{5}{2}$,-$\frac{9}{4}$);
②t1∈(0,1],t2∈(1,$\frac{5}{4}$),
此時同理可得a∈(-$\frac{9}{4}$,-1),
綜上可得a的范圍是(-$\frac{5}{2}$,-$\frac{9}{4}$)∪(-$\frac{9}{4}$,-1),
故答案為(-$\frac{5}{2}$,-$\frac{9}{4}$)∪(-$\frac{9}{4}$,-1).
點評 本題主要考查分段函數的應用,利用換元法結合函數奇偶性的對稱性,利用數形結合是解決本題的關鍵.綜合性較強.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
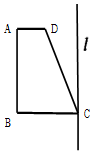 如圖,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD內過點C作l⊥CB,將梯形ABCD以l為軸旋轉一周
如圖,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD內過點C作l⊥CB,將梯形ABCD以l為軸旋轉一周查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | g(x)在區間[-$\frac{π}{12},\frac{π}{3}$]上的最小值為-1. | |
| B. | g(x)的圖象可由函數f(x)向上平移2個單位,在向右平移$\frac{π}{3}$個單位得到. | |
| C. | g(x)的圖象可由函數f(x)的圖象先向左平移$\frac{π}{3}$個單位得到. | |
| D. | g(x)的圖象可由函數f(x)的圖象先向右平移$\frac{π}{3}$個單位得到. |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com