
分析 由已知數列遞推式可得$\frac{n+1}{{a}_{n+1}}-1=\frac{1}{4}(\frac{n}{{a}_{n}}-1)$,即數列{$\frac{n}{{a}_{n}}-1$}是以-$\frac{1}{4}$為首項,以$\frac{1}{4}$為公比的等比數列,求出等比數列的通項公式,作和即可求得$\frac{1}{{a}_{1}}$+$\frac{2}{{a}_{2}}$+$\frac{3}{{a}_{3}}$+…+$\frac{2016}{{a}_{2016}}$.
解答 解:由an+1=$\frac{4(n+1){a}_{n}}{3{a}_{n}+n}$,得$\frac{{a}_{n+1}}{n+1}=\frac{4{a}_{n}}{3{a}_{n}+n}$,
∴$\frac{n+1}{{a}_{n+1}}=\frac{1}{4}•\frac{n}{{a}_{n}}+\frac{3}{4}$,則$\frac{n+1}{{a}_{n+1}}-1=\frac{1}{4}(\frac{n}{{a}_{n}}-1)$,
又$\frac{1}{{a}_{1}}-1=\frac{3}{4}-1=-\frac{1}{4}$.
∴數列{$\frac{n}{{a}_{n}}-1$}是以-$\frac{1}{4}$為首項,以$\frac{1}{4}$為公比的等比數列,
則$\frac{n}{{a}_{n}}-1=-\frac{1}{4}•(\frac{1}{4})^{n-1}$,$\frac{n}{{a}_{n}}=1-\frac{1}{{4}^{n}}$.
∴$\frac{1}{{a}_{1}}$+$\frac{2}{{a}_{2}}$+$\frac{3}{{a}_{3}}$+…+$\frac{2016}{{a}_{2016}}$=$1-\frac{1}{4}+1-\frac{1}{{4}^{2}}+…+1-\frac{1}{{4}^{2016}}$
=2016-($\frac{1}{4}+\frac{1}{{4}^{2}}+…+\frac{1}{{4}^{2016}}$)=$2016-\frac{\frac{1}{4}(1-\frac{1}{{4}^{2016}})}{1-\frac{1}{4}}$=$2015\frac{2}{3}+\frac{1}{3•{4}^{2016}}$.
故答案為:$2015\frac{2}{3}+\frac{1}{3•{4}^{2016}}$.
點評 本題考查數列遞推式,考查了等比關系的確定,考查等比數列前n項和的求法,是中檔題.


科目:高中數學 來源: 題型:解答題
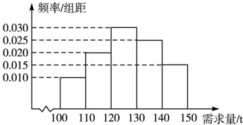 經銷商經銷某種農產品,在一個銷售季度內,每售出1t該產品獲利潤500元,未售出的產品,每1t虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了130t該農產品.以X(單位:t,100≤X≤150)表示下一個銷售季度內的市場需求量,T(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
經銷商經銷某種農產品,在一個銷售季度內,每售出1t該產品獲利潤500元,未售出的產品,每1t虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了130t該農產品.以X(單位:t,100≤X≤150)表示下一個銷售季度內的市場需求量,T(單位:元)表示下一個銷售季度內經銷該農產品的利潤.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3x+2y=0 | B. | 3x-2y=0 | C. | 2x+3y=0 | D. | 2x-3y=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com