
分析 (1)若a=0,b=3,求導數,令f′(x)=得x=0或2,即可求y=f(x)的切線中與y軸垂直的切線方程.
(2)得出函數f(x)在x=0處取得極大值,在x=2處取得極小值.函數f(x)在(t,t+3)上既能取到極大值,又能取到極小值,則只要t<0且t+3>2即可;
(3)問題轉化為b≤x+$\frac{lnx}{x}$+$\frac{1}{x}$在對任意的x∈[$\frac{1}{2}$,+∞)恒成立.令g(x)=x+$\frac{lnx}{x}$+$\frac{1}{x}$,則g′(x)=$\frac{{x}^{2}-lnx}{{x}^{2}}$.求出函數的最小值,即可得出結論.
解答 解:(1)當a=0,b=3時,f(x)=x3-3x2,f′(x)=3x2-6x,
令f′(x)=得x=0或2,∴y=0或-4;
(2)當a=0,b=3時,f(x)=x3-3x2,f′(x)=3x2-6x,
令令f′(x)=得x=0或2,根據導數的符號可以得出函數f(x)在x=0處取得極大值,在x=2處取得極小值.
函數f(x)在(t,t+3)上既能取到極大值,又能取到極小值,則只要t<0且t+3>2即可,
即只要-1<t<0即可.
所以t的取值范圍是(-1,0).
(3)當a=0時,$\frac{f(x)}{x}$+lnx+1≥0對任意的x∈[$\frac{1}{2}$,+∞)恒成立,
即x2-bx+lnx+1≥0對任意的x∈[$\frac{1}{2}$,+∞)恒成立,
也即b≤x+$\frac{lnx}{x}$+$\frac{1}{x}$在對任意的x∈[$\frac{1}{2}$,+∞)恒成立.
令g(x)=x+$\frac{lnx}{x}$+$\frac{1}{x}$,則g′(x)=$\frac{{x}^{2}-lnx}{{x}^{2}}$.
記m(x)=x2-lnx,則m′(x)=$\frac{2{x}^{2}-1}{x}$,
則這個函數在其定義域內有唯一的極小值點x=$\frac{\sqrt{2}}{2}$,故也是最小值點,
所以m(x)≥$\frac{1}{2}-ln\frac{\sqrt{2}}{2}$>0,從而g′(x)>0,
所以函數g(x)在[$\frac{1}{2}$,+∞)單調遞增.函數g(x)min=$\frac{5}{2}$-2ln2.
故只要b≤$\frac{5}{2}$-2ln2即可.所以b的取值范圍是(-∞,$\frac{5}{2}$-2ln2]. (8分)
點評 本題考查導數知識的綜合運用,考查導數的幾何意義、極值,考查恒成立問題,考查學生分析解決問題的能力,屬于中檔題.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
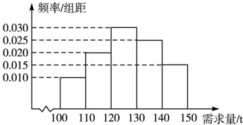 經銷商經銷某種農產品,在一個銷售季度內,每售出1t該產品獲利潤500元,未售出的產品,每1t虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了130t該農產品.以X(單位:t,100≤X≤150)表示下一個銷售季度內的市場需求量,T(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
經銷商經銷某種農產品,在一個銷售季度內,每售出1t該產品獲利潤500元,未售出的產品,每1t虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了130t該農產品.以X(單位:t,100≤X≤150)表示下一個銷售季度內的市場需求量,T(單位:元)表示下一個銷售季度內經銷該農產品的利潤.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -5<x<0或x>5 | B. | x<-5或x>5 | C. | -5<x<5 | D. | x<-5或0<x<5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com