
| 學生編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 數學分數x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分數y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
分析 (1)從25名男同學中選$\frac{25}{40}×8$位,從15名女同學中選$\frac{15}{40}×8$位,即可得出樣本的種數.
(2)①從8為同學中恰有3為同學的數學與物理均為優秀,從物理的4個優秀分數中選3個與數學優秀分數對應,種數是${A}_{4}^{3}$,然后將剩下的5個數學分數和物理分數任意對應,種數是${A}_{5}^{5}$,根據乘法原理可得滿足條件的種數,這8位同學的物理分數和數學分數分布對應的種數共有${A}_{8}^{8}$種,即可得出所求的概率.
②設y與x的線性回歸方程是$\stackrel{∧}{y}$=bx+a,根據所給數據,可以計算出$b≈\frac{688}{1050}≈0.66$,a=84.875-0.66×77.5≈33.73,可得y與x的線性回歸方程.
解答 解:(1)從25名男同學中選$\frac{25}{40}×8$=5位,從15名女同學中選$\frac{15}{40}×8$=3位.
可以得到${∁}_{25}^{5}$×${∁}_{15}^{3}$個不同的樣本.
(2)①從8為同學中恰有3為同學的數學與物理均為優秀,從物理的4個優秀分數中選3個與數學優秀分數對應,種數是${A}_{4}^{3}$,然后將剩下的5個數學分數和物理分數任意對應,種數是${A}_{5}^{5}$,根據乘法原理可得:滿足條件的種數是${A}_{4}^{3}{A}_{5}^{5}$,這8位同學的物理分數和數學分數分布對應的種數共有${A}_{8}^{8}$種,故所求的概率P=$\frac{{A}_{4}^{3}•{A}_{5}^{5}}{{A}_{8}^{8}}$=$\frac{1}{14}$.
②設y與x的線性回歸方程是$\stackrel{∧}{y}$=bx+a,根據所給數據,可以計算出$b≈\frac{688}{1050}≈0.66$,a=84.875-0.66×77.5≈33.73,所以y與x的線性回歸方程是$\stackrel{∧}{y}$=0.66x+33.73.
點評 本題考查了分層抽樣、組合計算公式、乘法原理、古典概率計算公式、線性回歸方程,考查了推理能力與計算能力,屬于中檔題.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:選擇題
| A. | 大前提錯誤 | B. | 小前提錯誤 | C. | 推理形式錯誤 | D. | 結論正確 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | |z1|<0且|z2|<1 | B. | |z1|<1或|z2|<1 | C. | |z1|=1且|z2|=1 | D. | |z1|=1或|z2|=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
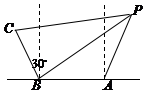 為捍衛釣魚島及其附屬島嶼的領土主權,中國派出艦船“唐山號”、“石家莊號”和“邯鄲號”在釣魚島領海巡航.某日,正巡邏在A處的“唐山號”突然發現來自P處的疑似敵艦的某信號,發現信號時“石家莊號”和“邯鄲號”正分別位于如圖所示的B、C兩處,其中A在B的正東方向相距6海里處,C在B的北偏西30°方向相距4海里處.由于B、C比A距P更遠,因此,4秒后B、C才同時發現這一信號(該信號的傳播速度為每秒1海里),試確定疑似敵艦相對于A點“唐山號”的位置.
為捍衛釣魚島及其附屬島嶼的領土主權,中國派出艦船“唐山號”、“石家莊號”和“邯鄲號”在釣魚島領海巡航.某日,正巡邏在A處的“唐山號”突然發現來自P處的疑似敵艦的某信號,發現信號時“石家莊號”和“邯鄲號”正分別位于如圖所示的B、C兩處,其中A在B的正東方向相距6海里處,C在B的北偏西30°方向相距4海里處.由于B、C比A距P更遠,因此,4秒后B、C才同時發現這一信號(該信號的傳播速度為每秒1海里),試確定疑似敵艦相對于A點“唐山號”的位置.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com