
| X | 6 | 8 | 10 | 12 |
| Y | 2 | 3 | 5 | 6 |
分析 (1)根據表中數據畫出散點圖即可;
(2)計算回歸系數,求出對應的線性回歸方程;
(3)利用回歸系數計算x=14時y的值.
解答 解:(1)畫出上表數據的散點圖,如圖所示;…(3分)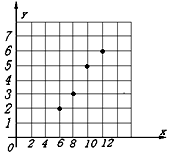
(2)計算$\sum_{i=1}^{n}$xiyi═6×2+8×3+10×5+12×6=158,
$\overline{x}$=$\frac{1}{4}$×(6+8+10+12)=9,
$\overline{y}$=$\frac{1}{4}$×(2+3+5+6)=4,
$\sum_{i=1}^{n}$${{x}_{i}}^{2}$=62+82+102+122=344,
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{158-4×9×4}{344-4{×9}^{2}}$=$\frac{14}{20}$=0.7,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=4-0.7×9=-2.3,
故線性回歸方程為:y=0.7x-2.3.…(10分)
(3)當x=14時,y=0.7×14-2.3=7.5,
即預測記憶力為14的同學判斷力為14.
點評 本題考查了線性回歸方程的應用問題,也考查了散點圖的應用問題,是基礎題目.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $2\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
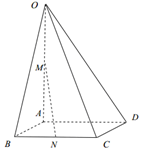 如圖,在四棱錐O-ABCD中,底面ABCD是四邊長為$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M為OA的中點,N為BC的中點.
如圖,在四棱錐O-ABCD中,底面ABCD是四邊長為$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M為OA的中點,N為BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2k-1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,四棱錐C-ABB1A1內接于圓柱OO1,且A1A,B1B都垂直于底面圓O,BC過底面圓心O,M,N分別是棱AA1,CB1的中點,MN⊥平面CBB1.
如圖,四棱錐C-ABB1A1內接于圓柱OO1,且A1A,B1B都垂直于底面圓O,BC過底面圓心O,M,N分別是棱AA1,CB1的中點,MN⊥平面CBB1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com