
分析 由題意設|PC|:|CF|=1:t,由拋物線的焦半徑公式比例關系求得P點坐標,則S△PFB=(1+t)2$\sqrt{2}$,根據三角形的面積公式,列方程即可求得t的值.
解答 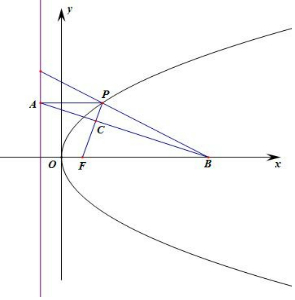 解:設拋物線E:y2=4x的焦點為F(1,0),準線x=-1,設P(xP,yP),
解:設拋物線E:y2=4x的焦點為F(1,0),準線x=-1,設P(xP,yP),
設|PC|:|CF|=1:t,則t丨PC丨=丨CF丨,丨AP丨=丨PF丨=xP+1,
由AB∥x軸,則丨AP丨:丨FB丨=|PC|:|CF|=$\frac{1}{t}$,即$\frac{1+{x}_{P}}{7-1}$=$\frac{1}{t}$,
則xP=$\frac{6-t}{t}$,yP=2$\sqrt{\frac{6-t}{t}}$,
由|PC|:|CF|=1:t,則S△PBC:S△FBC=1:t,
∴S△PFB=(1+t)2$\sqrt{2}$,
∴$\frac{1}{2}$×丨FB丨×yP=(1+t)2$\sqrt{2}$,即$\frac{1}{2}$×6×2$\sqrt{\frac{6-t}{t}}$=(1+t)2$\sqrt{2}$,
整理得:2t3+4t2+11t-54=0,解得:t=2,
∴|PC|:|CF|=$\frac{1}{2}$,
故答案為:$\frac{1}{2}$.
點評 本題考查拋物線的性質,考查相似三角形的性質,考查數形結合思想,考查計算能力,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
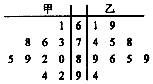 甲、乙兩位同學參加數學競賽培訓,培訓期間共參加了10次模擬考試,根據考試成績,得到如下圖所示的莖葉圖.規定模擬考試成績不低于81分為優秀等次.
甲、乙兩位同學參加數學競賽培訓,培訓期間共參加了10次模擬考試,根據考試成績,得到如下圖所示的莖葉圖.規定模擬考試成績不低于81分為優秀等次.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com