
【題目】已知半圓![]() :
:![]() ,
,![]() 、
、![]() 分別為半圓
分別為半圓![]() 與
與![]() 軸的左、右交點,直線
軸的左、右交點,直線![]() 過點
過點![]() 且與
且與![]() 軸垂直,點
軸垂直,點![]() 在直線
在直線![]() 上,縱坐標為
上,縱坐標為![]() ,若在半圓
,若在半圓![]() 上存在點
上存在點![]() 使
使![]() ,則
,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
根據(jù)題意,設PQ與x軸交于點T,分析可得在Rt△PBT中,|BT|![]() |PB|
|PB|![]() |t|,分p在x軸上方、下方和x軸上三種情況討論,分析|BT|的最值,即可得t的范圍,綜合可得答案.
|t|,分p在x軸上方、下方和x軸上三種情況討論,分析|BT|的最值,即可得t的范圍,綜合可得答案.
根據(jù)題意,設PQ與x軸交于點T,則|PB|=|t|,
由于BP與x軸垂直,且∠BPQ![]() ,則在Rt△PBT中,
,則在Rt△PBT中,
|BT|![]() |PB|
|PB|![]() |t|,
|t|,
當P在x軸上方時,PT與半圓有公共點Q,PT與半圓相切時,|BT|有最大值3,此時t有最大值![]() ,
,
當P在x軸下方時,當Q與A重合時,|BT|有最大值2,|t|有最大值![]() ,則t取得最小值
,則t取得最小值![]() ,
,
t=0時,P與B重合,不符合題意,
則t的取值范圍為[![]() ,0)
,0)![]() ];
];
故選:A.



 星級口算天天練系列答案
星級口算天天練系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在圓心角為直角的扇形OAB區(qū)域中,M、N分別為OA、OB的中點,在M、N兩點處各有一個通信基站,其信號的覆蓋范圍分別為以OA、OB為直徑的圓,在扇形OAB內(nèi)隨機取一點,則此點無信號的概率是![]()
![]()
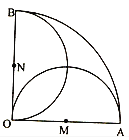
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線![]() 的一個焦點是
的一個焦點是![]() ,且
,且![]()
(1)求雙曲線![]() 的方程
的方程
(2)設經(jīng)過焦點![]() 的直線
的直線![]() 的一個法向量為
的一個法向量為![]() ,當直線
,當直線![]() 與雙曲線
與雙曲線![]() 的右支相交于不同的兩點
的右支相交于不同的兩點![]() 時,求實數(shù)
時,求實數(shù)![]() 的取值范圍
的取值范圍
(3)設(2)中直線![]() 與雙曲線
與雙曲線![]() 的右支相交于
的右支相交于![]() 兩點,問是否存在實數(shù)
兩點,問是否存在實數(shù)![]() ,使得
,使得![]() 為銳角?若存在,請求出
為銳角?若存在,請求出![]() 的范圍;若不存在,請說明理由
的范圍;若不存在,請說明理由
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,AD與BC是四面體ABCD中互相垂直的棱,BC=2. 若AD=2c,且AB+BD=AC+CD=2a,其中a、c為常數(shù),則四面體ABCD的體積的最大值是 .
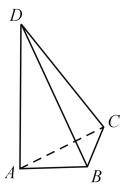
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在![]() 的二項展開式中,所有項的二項式系數(shù)之和為
的二項展開式中,所有項的二項式系數(shù)之和為![]() .
.
(1)求展開式的常數(shù)項:
(2)求展開式中所有奇數(shù)項的系數(shù)和.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列說法中正確的個數(shù)是( )
①相關系數(shù)![]() 用來衡量兩個變量之間線性關系的強弱,
用來衡量兩個變量之間線性關系的強弱,![]() 越接近于1,相關性越弱;
越接近于1,相關性越弱;
②回歸直線![]() 過樣本點中心
過樣本點中心![]() ;
;
③相關指數(shù)![]() 用來刻畫回歸的效果,
用來刻畫回歸的效果,![]() 越小,說明模型的擬合效果越不好.
越小,說明模型的擬合效果越不好.
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,正方形![]() 的邊長為
的邊長為![]() 米,圓
米,圓![]() 的半徑為
的半徑為![]() 米,圓心是正方形的中心,點
米,圓心是正方形的中心,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,若線段
上,若線段![]() 與圓
與圓![]() 有公共點,則稱點
有公共點,則稱點![]() 在點
在點![]() 的“盲區(qū)”中,已知點
的“盲區(qū)”中,已知點![]() 以
以![]() 米/秒的速度從
米/秒的速度從![]() 出發(fā)向
出發(fā)向![]() 移動,同時,點
移動,同時,點![]() 以
以![]() 米/秒的速度從
米/秒的速度從![]() 出發(fā)向
出發(fā)向![]() 移動,則在點
移動,則在點![]() 從
從![]() 移動到
移動到![]() 的過程中,點
的過程中,點![]() 在點
在點![]() 的盲區(qū)中的時長約________秒(精確到
的盲區(qū)中的時長約________秒(精確到![]() ).
).
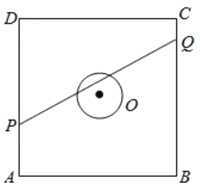
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 短軸的一個頂點到一個焦點的距離等于
短軸的一個頂點到一個焦點的距離等于![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設經(jīng)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,點
兩點,點![]() .
.
①若對任意直線![]() 總存在點
總存在點![]() ,使得
,使得![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍;
的取值范圍;
②設點![]() 為橢圓
為橢圓![]() 的左焦點,若點
的左焦點,若點![]() 為
為![]() 的外心,求實數(shù)
的外心,求實數(shù)![]() 的值.
的值.
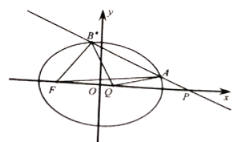
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com