
| 優秀 | 非優秀 | 總計 | |
| 甲班 | a=10 | b=45 | a+b=55 |
| 乙班 | c=20 | d=30 | c+d=50 |
| 合計 | a+c=30 | b+d=75 | 105 |
| P(x2>k) | 0.010 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.82 |
分析 (I) 根據全部105人中隨機抽取1人為優秀的概率為$\frac{2}{7}$,則優秀人數=$105×\frac{2}{7}$=30,可得c=30-10=20.∴c+d=50,
a+b=105-50=55,b=55-10=45.進而得出下表:根據列聯表中的數據,得到K2.
(II)根據分層抽樣可得:從甲班中應抽取人數=$\frac{10}{30}×9$=3,從乙班中應抽取人數=9-3=6.然后再選派3人參加市里的數學競賽,記甲班優秀生被派出的人數為X,則X=0,1,2,3.P(X=k)=$\frac{{∁}_{3}^{k}{∁}_{6}^{3-k}}{{∁}_{9}^{3}}$.
解答 解:(I) 根據全部105人中隨機抽取1人為優秀的概率為$\frac{2}{7}$,
則優秀人數=$105×\frac{2}{7}$=30,可得c=30-10=20.
∴c+d=50,
a+b=105-50=55,b=55-10=45.進而得出下表:
| 優秀 | 非優秀 | 總計 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合計 | 30 | 75 | 105 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{20}{84}$ | $\frac{45}{84}$ | $\frac{18}{84}$ | $\frac{1}{84}$ |
點評 本題考查了頻數分布表、“列聯表”、獨立性檢驗計算公式、分層抽樣、超幾何分布列計算公式及其數學期望,考查了推理能力與計算能力,屬于中檔題.


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:高中數學 來源: 題型:選擇題
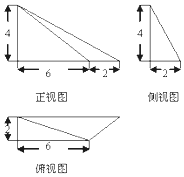
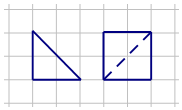 如圖,網格紙上小正方形的邊長為1,粗線畫出的是某幾何體的正視圖(等腰直角三角形)和側視圖,且該幾何體的體積為$\frac{8}{3}$,則該幾何體的俯視圖可以是( )
如圖,網格紙上小正方形的邊長為1,粗線畫出的是某幾何體的正視圖(等腰直角三角形)和側視圖,且該幾何體的體積為$\frac{8}{3}$,則該幾何體的俯視圖可以是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{56}{3}$ | B. | $\frac{112}{3}$ | C. | $\frac{119}{3}$ | D. | $\frac{128}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
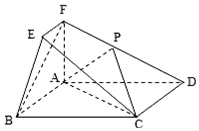 在如圖所示的幾何體中,四邊形ABCD為矩形,平面ABCD⊥平面ABEF,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,點P在棱DF上.
在如圖所示的幾何體中,四邊形ABCD為矩形,平面ABCD⊥平面ABEF,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,點P在棱DF上.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com