
 如圖,已知AB是半徑為2的半球O的直徑,P,D為球面上的兩點且∠DAB=∠PAB=60°,$PD=\sqrt{6}$.
如圖,已知AB是半徑為2的半球O的直徑,P,D為球面上的兩點且∠DAB=∠PAB=60°,$PD=\sqrt{6}$.分析 (1)在△PAB中,過P作PH⊥AB于點H,連HD.證明DH⊥AB,PH⊥HD.推出PH⊥平面ABD,然后證明平面PAB⊥平面ABD.
(2)由(1)可知HB,HD,HP兩兩垂直,故以H為原點,HB,HD,HP所在直線分別為x軸,y軸,z軸,求出相關點的坐標求出平面APD的法向量,平面APB的法向量,利用空間向量的數量積求解二面角B-AP-D的余弦值即可.
解答 解:(1)證明:在△PAB中,過P作PH⊥AB于點H,連HD.
由Rt△APB≌Rt△ADB可知DH⊥AB,且$PH=DH=\sqrt{3},AH=1$,
又 PH2+HD2=3+3=6=PD2,∴PH⊥HD.
又AB∩HD=H,∴PH⊥平面ABD,又PH?平面PAB,
∴平面PAB⊥平面ABD.
(2)由(1)可知HB,HD,HP兩兩垂直,
故以H為原點,HB,HD,HP所在直線分別為x軸,y軸,z軸,如圖建立空間直角坐標系,可知$A({-1,0,0}),B({3,0,0}),D({0,\sqrt{3},0}),P({0,0,\sqrt{3}})$.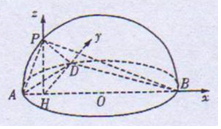
設平面APD的法向量為$\overrightarrow{m}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=0}\\{\overrightarrow{m}•\overrightarrow{AP}=0}\end{array}\right.$,即$\left\{{\begin{array}{l}{({x,y,z})({1,\sqrt{3},0})=0}\\{({x,y,z})({1,0,\sqrt{3}})=0}\end{array}}\right.$,
∴$\left\{{\begin{array}{l}{x+\sqrt{3}y=0}\\{x+\sqrt{3}z=0}\end{array}}\right.$,
令$x=-\sqrt{3}$,則得y=z=1,∴$m=({-\sqrt{3},1,1})$,
又平面APB的法向量$\overrightarrow{n}$=(0,1,0),
∴cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
而二面角B-AP-D與m,n的夾角相等,
因此所求的二面角B-AP-D的余弦值為$\frac{{\sqrt{5}}}{5}$.
點評 本題考查二面角的平面角的求法,平面與平面垂直的判定定理的應用,考查空間想象能力以及邏輯推理能力計算能力.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:選擇題
| A. | (2,3) | B. | [1,+∞) | C. | [2,3] | D. | [1,2]∪[3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{-1-\frac{1}{e},1-\frac{1}{e}}]$ | B. | $({-1-\frac{1}{e},-1})∪\left\{{1-\frac{1}{e}}\right\}$ | ||
| C. | $({1-\frac{1}{e},+∞})$ | D. | $({-1-\frac{1}{e},-1})∪[{1-\frac{1}{e},+∞})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,將繪有函數$f(x)=\sqrt{3}sin({ωx+\frac{5π}{6}})({ω>0})$部分圖象的紙片沿x軸折成直二面角,若AB之間的空間距離為$\sqrt{15}$,則f(-1)=( )
如圖,將繪有函數$f(x)=\sqrt{3}sin({ωx+\frac{5π}{6}})({ω>0})$部分圖象的紙片沿x軸折成直二面角,若AB之間的空間距離為$\sqrt{15}$,則f(-1)=( )| A. | -1 | B. | 1 | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com