
分析 將a+b變形為=($\frac{1}{a+1}$+$\frac{1}{b}$)(a+1+b)-1,展開,利用基本不等式解之.
解答 解:已知a>0,b>0,$\frac{1}{a+1}$+$\frac{1}{b}$=1,
則a+b=($\frac{1}{a+1}$+$\frac{1}{b}$)(a+1+b)-1=2+$\frac{b}{a+1}+\frac{a+1}{b}$-1≥1+2$\sqrt{\frac{b}{a+1}•\frac{a+1}{b}}$=3,
當且僅當a+1=b時等號成立;
故答案為:3
點評 本題考查了利用基本不等式求代數式的最值;關鍵是變形為能夠利用基本不等式的形式.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | $\frac{1}{11}$ | C. | -$\frac{1}{13}$ | D. | -$\frac{1}{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖,直角△ABC中,AB=1,BC=2,∠ABC=90°,作△ABC的內接正方形BEFB1,再作△B1FC的內接正方形B1E1F1B2,…,依次下去,所有正方形的面積依次構成數列{an},其前n項和為$\frac{4}{5}$$[1-(\frac{4}{9})^{n}]$.
如圖,直角△ABC中,AB=1,BC=2,∠ABC=90°,作△ABC的內接正方形BEFB1,再作△B1FC的內接正方形B1E1F1B2,…,依次下去,所有正方形的面積依次構成數列{an},其前n項和為$\frac{4}{5}$$[1-(\frac{4}{9})^{n}]$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
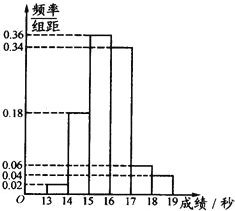 某班50名學生在一次百米測試中,成績全部介于13秒與19秒之間,如圖是測試成績頻率分布直方圖.成績小于17秒的學生人數為( )
某班50名學生在一次百米測試中,成績全部介于13秒與19秒之間,如圖是測試成績頻率分布直方圖.成績小于17秒的學生人數為( )| A. | 45 | B. | 35 | C. | 17 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | “f(0)=0”是“函數f(x)是奇函數”的充要條件 | |
| B. | 命題“若$α=\frac{π}{6}$,則$sinα=\frac{1}{2}$”的否命題是“若$α≠\frac{π}{6}$,則$sinα≠\frac{1}{2}$” | |
| C. | 若p∧q為假命題,則p,q均為假命題 | |
| D. | 若p:?x0∈R,$x_0^2-{x_0}-1>0$,則?p:?x∈R,x2-x-1<0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10000001110(2) | B. | 10000011110(2) | C. | 100000011101(2) | D. | 10000001100(2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com