
分析 (1)由等差數列的性質及三角形內角和定理可求$B=\frac{π}{3}$,由正弦定理可求a=$\frac{3c}{4}$,進而利用余弦定理可得c的值.
(2)由正弦定理,可得a=$\frac{2\sqrt{13}}{\sqrt{3}}$sinA,c=$\frac{2\sqrt{13}}{\sqrt{3}}$sinC,利用三角函數恒等變換的應用化簡可得a+c=2$\sqrt{13}$sin(A+$\frac{π}{6}$),由$0<A<\frac{2π}{3}$,可求范圍$\frac{π}{6}<A+\frac{π}{6}<\frac{5π}{6}$,進而利用正弦函數的性質可求最大值.
解答 解:(1)∵由角A,B,C的度數成等差數列,得2B=A+C.
又∵A+B+C=π,
∴$B=\frac{π}{3}$.
∴由正弦定理,可得:3c=4a,即a=$\frac{3c}{4}$,
∴由余弦定理,可得:b2=a2+c2-2accosB,即:13=($\frac{3c}{4}$)2+c2-2×$\frac{3c}{4}×c×\frac{1}{2}$,解得:c=4.
(2)由正弦定理,可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=$\frac{\sqrt{13}}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{13}}{\sqrt{3}}$,
∴a=$\frac{2\sqrt{13}}{\sqrt{3}}$sinA,c=$\frac{2\sqrt{13}}{\sqrt{3}}$sinC,
∴$a+c=\frac{{2\sqrt{13}}}{{\sqrt{3}}}({sinA+sinC})=\frac{{2\sqrt{13}}}{{\sqrt{3}}}[{sinA+sin({A+B})}]=\frac{{2\sqrt{13}}}{{\sqrt{3}}}[{sinA+sin({A+\frac{π}{3}})}]$=$\frac{{2\sqrt{13}}}{{\sqrt{3}}}({\frac{3}{2}sinA+sin\frac{{\sqrt{3}}}{2}cosA})=2\sqrt{13}sin({A+\frac{π}{6}})$.
由$0<A<\frac{2π}{3}$,得$\frac{π}{6}<A+\frac{π}{6}<\frac{5π}{6}$.
所以當$A+\frac{π}{6}=\frac{π}{2}$,即$A=\frac{π}{3}$時,${({a+c})_{max}}=2\sqrt{13}$.
點評 本題主要考查了等差數列的性質,三角形內角和定理,正弦定理,余弦定理,三角函數恒等變換的應用,正弦函數的圖象和性質在解三角形中的綜合應用,考查了計算能力和轉化思想,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 函數f(x)+x2是奇函數 | B. | 函數f(x)+|x|是偶函數 | ||
| C. | 函數x2f(x)是奇函數 | D. | 函數|x|f(x)是偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x∈R,sinx≤1 | B. | ?x∈R,sinx>1 | C. | ?x∈R,sinx≥1 | D. | ?x∈R,sinx>1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
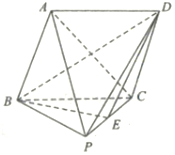 如圖,在四棱錐P-ABCD中,底面ABCD是菱形,側面PBC是直角三角形,∠PCB=90°,點E是PC的中點,且平面PBC⊥平面ABCD.
如圖,在四棱錐P-ABCD中,底面ABCD是菱形,側面PBC是直角三角形,∠PCB=90°,點E是PC的中點,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com