
分析 (1)求導數,利用斜率為$-\frac{1}{3}$,求出切點坐標,即可求滿足斜率為$-\frac{1}{3}$的曲線的切線方程;
(2)設過該點的切線切點為$B(b,\frac{1}{b})$,求導數,即可求曲線過點P(1,0)的切線方程.
解答 解:(1)設切點為$A(a,\frac{1}{a})$,
則切線斜率為$k=y'{|_{c=a}}=-\frac{1}{a^2}$,…(1分)
所以$-\frac{1}{a^2}=-\frac{1}{3}$,解得$a=±\sqrt{3}$,…(2分)
所以,切點坐標為$(\sqrt{3},\frac{{\sqrt{3}}}{3})$或$(-\sqrt{3},-\frac{{\sqrt{3}}}{3})$,…(3分)
于是,切線方程為$y-\frac{{\sqrt{3}}}{3}=-\frac{1}{3}(x-\sqrt{3})$或$y+\frac{{\sqrt{3}}}{3}=-\frac{1}{3}(x+\sqrt{3})$,
整理得,$x+3y-2\sqrt{3}=0$或$x+3y+2\sqrt{3}=0$.…(5分)
(2)顯然點P(1,0)不在曲線$y=\frac{1}{x}$上,…(6分)
則可設過該點的切線切點為$B(b,\frac{1}{b})$,
而斜率$k=y'{|_{k=b}}=-\frac{1}{b^2}$,…(7分)
于是,切線方程為$y-\frac{1}{b}=-\frac{1}{b^2}(x-b)$,①…(8分)
將P(1,0)坐標代入方程①得$-\frac{1}{b}=-\frac{1}{b^2}(1-b)$,解得$b=\frac{1}{2}$,…(9分)
把$b=\frac{1}{2}$代入方程①,并整理得切線方程為4x+y-4=0.…(10分)
點評 本題考查導數幾何意義的運用,考查學生的計算能力,正確求導是關鍵.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{6}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{36}=1$ | C. | $\frac{x^2}{36}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{49}+\frac{y^2}{9}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
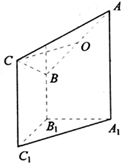 如圖是一個直三棱柱(以A1B1C1為底面)被一平面所截得到的幾何體,截面為ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.
如圖是一個直三棱柱(以A1B1C1為底面)被一平面所截得到的幾何體,截面為ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
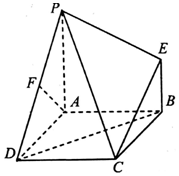 如圖,四邊形ABCD是正方形,PA⊥平面ABCD,EB∥PA,AB=PA=4,EB=2,F為PD的中點.
如圖,四邊形ABCD是正方形,PA⊥平面ABCD,EB∥PA,AB=PA=4,EB=2,F為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若l∥α,則l平行于α內的所有直線 | B. | 若m?α,l?β且l⊥m,則α⊥β | ||
| C. | 若l?β,l⊥α,則α⊥β | D. | 若m?α,l?β且α∥β,則m∥l |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com