
分析 (1)利用導數,我們可以確定函數的單調性,這樣就可求f(x)的極大值;(2)求導數,再進行類討論,利用導數的正負,確定函數的單調性.
解答 解:(1)當m=2時,f(x)=$\frac{5}{2}$lnx+$\frac{1}{x}$-x,
f′(x)=-$\frac{(x-2)(2x-1)}{{2x}^{2}}$(x>0),
f′(x)<0,可得0<x<$\frac{1}{2}$或x>2;
令f′(x)>0,可得$\frac{1}{2}$<x<2,
∴f(x)在(0,$\frac{1}{2}$)和(2,+∞)上單調遞減,在($\frac{1}{2}$,2)單調遞增
故f(x)極大=f(2)=$\frac{5}{2}$ln2-$\frac{3}{2}$;
(2)f′(x)=-$\frac{(x-m)(x-\frac{1}{m})}{{x}^{2}}$,x>0,m>0)
①當0<m<1時,則$\frac{1}{m}$>1,故x∈(0,m),f′(x)<0;
x∈(m,1)時,f′(x)>0
此時f(x)在(0,m)上單調遞減,在(m,1)單調遞增;
②當m=1時,則$\frac{1}{m}$=1,故x∈(0,1),有f′(x)=-$\frac{{(x-1)}^{2}}{{x}^{2}}$<0恒成立,
此時f(x)在(0,1)上單調遞減;
③當m>1時,則0<$\frac{1}{m}$<1,
故x∈(0,$\frac{1}{m}$)時,f′(x)<0;x∈($\frac{1}{m}$,1)時,f′(x)>0,
此時f(x)在(0,$\frac{1}{m}$)上單調遞減,在($\frac{1}{m}$,1)單調遞增.
點評 用導數,我們可解決曲線的切線問題,函數的單調性、極值與最值,正確求導是我們解題的關鍵.


科目:高中數學 來源: 題型:解答題
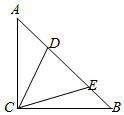 如圖,等腰直角三角形區域ABC中,∠ACB=90°,BC=AC=1百米.現準備劃出一塊三角形區域CDE,其中D,E均在斜邊AB上,且∠DCE=45°.記三角形CDE的面積為S.
如圖,等腰直角三角形區域ABC中,∠ACB=90°,BC=AC=1百米.現準備劃出一塊三角形區域CDE,其中D,E均在斜邊AB上,且∠DCE=45°.記三角形CDE的面積為S.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x≤-1} | B. | {x|-1≤x≤0} | C. | {x|0≤x≤1} | D. | {x|1≤x≤2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1-e2]∪[e2-1,+∞) | B. | [1-e2,e2-1] | ||
| C. | (-∞,e-2-1]∪[1-e-2,+∞) | D. | [e-2-1,1-e-2] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com