
| A. | $[-1,-\frac{1}{3}]$ | B. | $[-\frac{1}{3},\frac{1}{3}]$ | C. | [-1,1] | D. | $[-1,\frac{1}{3}]$ |
分析 求出函數f(x)的導數f′(x)=x-$\frac{1}{3}$sin2xt+tsinx在R上單調遞增可轉化為f″(x)=-$\frac{4}{3}$cos2x+tcosx+$\frac{5}{3}$≥0,在R上恒成立,利用分離參數法即可求解.
解答 解:f′(x)=x-$\frac{1}{3}$sin2xt+tsinx在R上單調遞增,
即f″(x)=-$\frac{4}{3}$cos2x+tcosx+$\frac{5}{3}$≥0,在R上恒成立,
令m=cosx,m∈[-1,1],-$\frac{4}{3}$m2+tm+$\frac{5}{3}$≥0⇒tm≥$\frac{4}{3}$m2-$\frac{5}{3}$,
當m=0時,成立;當m∈(0,1]時,t≥$\frac{4}{3}$m-$\frac{5}{3m}$,
函數g(m)=$\frac{4}{3}$m-$\frac{5}{3m}$在(0,1]上是增函數,
∴t≥g(1)=-$\frac{1}{3}$;當m∈[-1,0)時,t≤$\frac{4}{3}$m-$\frac{5}{3m}$,
∵函數g(m)=$\frac{4}{3}$m-$\frac{5}{3m}$在[-1,0(上是增函數,t≤g(-1)=$\frac{1}{3}$,
綜上則實數t的取值范圍為[-$\frac{1}{3},\frac{1}{3}$].
故選B.
點評 本題考查了三角函數的變形以及由函數單調性的性質求參數的范圍.


科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1) | B. | (-∞,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 空氣污染,又稱為大氣污染,是指由于人類活動或自然過程引起某些物質進入大氣中,呈現出足夠的 濃度,達到足夠的時間,并因此危害了人體的舒適、健康和福利或環境的現象.全世界也越來越關注環境保護問題.
空氣污染,又稱為大氣污染,是指由于人類活動或自然過程引起某些物質進入大氣中,呈現出足夠的 濃度,達到足夠的時間,并因此危害了人體的舒適、健康和福利或環境的現象.全世界也越來越關注環境保護問題.| 空氣污染指數 (單位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 監測點個數 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
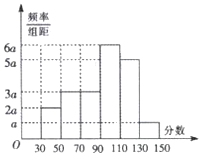 從某市高三數學考試成績中,隨機抽取了60名學生的成績得到頻率分布直方圖如圖:
從某市高三數學考試成績中,隨機抽取了60名學生的成績得到頻率分布直方圖如圖:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 容量,方差 | B. | 容量,平均數 | C. | 平均數,容量 | D. | 標準差,平均數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=-x2-2x+12 | B. | f(x)=x2-2x+10 | C. | f(x)=-x2+2x+8 | D. | f(x)=x2+2x+6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 無窮多個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com