
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 溫差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 發芽數y(顆) | 23 | 25 | 30 | 26 | 16 |
分析 (1)求出抽到相鄰兩組數據的事件概率,利用對立事件的概率計算抽到不相鄰兩組數據的概率值;
(2)由表中數據,利用公式計算回歸直線方程的系數,寫出回歸直線方程,利用方程計算并判斷所得到的線性回歸方程是否可靠.
解答 解:(1)設抽到不相鄰兩組數據為事件A,因為從5組數據中選取2組數據共有10種情況,
每種情況都是等可能出現的,其中抽到相鄰兩組數據的情況有4種,
所以$P(A)=1-\frac{4}{10}=\frac{3}{5}$;
(2)由數據,求得$\overline{x}$=$\frac{1}{5}$×(10+11+13+12+8)=10.8,
$\overline{y}$=$\frac{1}{5}$×(23+25+30+26+16)=24;
由公式,求得
$\sum_{i=1}^{5}$(xiyi)=10×23+11×25+13×30+12×26+8×16=1335,
$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=102+112+132+122+82=598;
所以$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$=$\frac{5}{2}$,
$\widehata=\overline y-\widehatb\overline x$=-3;
所以y關于x的線性回歸方程是$\overline y=\frac{5}{2}x-3$;
當x=10時,$\widehaty=\frac{5}{2}×10-3=22$,|22-23|<2;
同樣,當x=8時,$\widehaty=\frac{5}{2}×8-3=17$,|17-16|<2;
所以,該研究所得到的線性回歸方程是可靠的.
點評 本題考查了等可能事件的概率與回歸直線方程的應用問題,也考查了計算能力的應用問題,是綜合性題目.


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數$f(x)={x^2}-3\left|x\right|+\frac{1}{4}(x∈R)$
已知函數$f(x)={x^2}-3\left|x\right|+\frac{1}{4}(x∈R)$查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
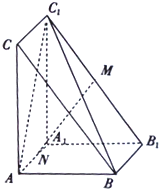 如圖,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分別為B1C1、AA1的中點.
如圖,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分別為B1C1、AA1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-2,2] | B. | [-3,2) | C. | [-3,2)∪(3,4] | D. | (3,4] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0<a<$\frac{16}{3}$ | B. | a<$\frac{16}{3}$ | C. | a<0或a>$\frac{16}{3}$ | D. | a≤$\frac{16}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com