
已知函數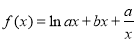 (
(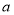 、
、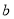 為常數),在
為常數),在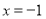 時取得極值.
時取得極值.
(1)求實數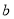 的取值范圍;
的取值范圍;
(2)當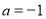 時,關于
時,關于 的方程
的方程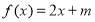 有兩個不相等的實數根,求實數
有兩個不相等的實數根,求實數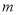 的取值范圍;
的取值范圍;
(3)數列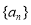 滿足
滿足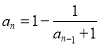 (
(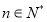 且
且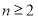 ),
),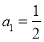 ,數列
,數列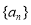 的前
的前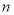 項和為
項和為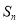 ,
,
求證: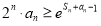 (
(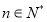 ,
,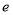 是自然對數的底).
是自然對數的底).
(1)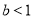 且
且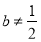 ;(2)
;(2)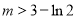 ;(3)詳見解析.
;(3)詳見解析.
【解析】
試題分析:(1)求實數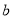 的取值范圍,因為函數
的取值范圍,因為函數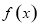 在
在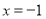 時取得極值,故
時取得極值,故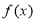 在
在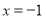 有定義,得
有定義,得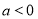 ,可對函數
,可對函數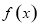 求導得,
求導得,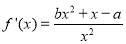 ,則
,則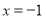 是
是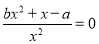 的根,這樣可得
的根,這樣可得 的關系是,再由
的關系是,再由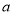 的范圍可求得
的范圍可求得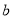 的取值范圍;(2)當
的取值范圍;(2)當 時,關于
時,關于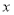 的方程
的方程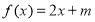 有兩個不相等的實數根,求實數
有兩個不相等的實數根,求實數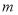 的取值范圍,當
的取值范圍,當 時,由
時,由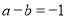 得
得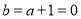 ,代入得
,代入得
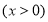 ,對
,對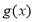 求導,判斷單調性,即可得函數
求導,判斷單調性,即可得函數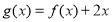 的最小值;(3)求證:
的最小值;(3)求證: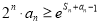 ,即證
,即證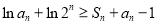 ,因此需求出數列
,因此需求出數列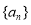 的通項公式及前
的通項公式及前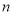 項和為
項和為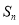 ,由數列
,由數列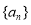 滿足
滿足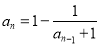 (
(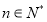 且
且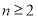 ),
),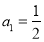 ,得
,得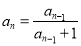 ,即
,即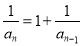 ,可求得
,可求得 ,它的前
,它的前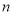 項和為
項和為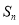 不好求,由此可利用式子中出現
不好求,由此可利用式子中出現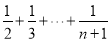 代換
代換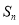 ,由(2)知
,由(2)知 ,令
,令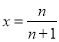 得,
得,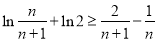 ,
,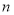 取
取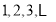 ,疊加可證得結論.
,疊加可證得結論.
試題解析:(1) ∵
∵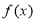 在
在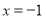 有定義 ∴
有定義 ∴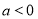
∴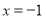 是方程
是方程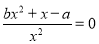 的根,且不是重根
的根,且不是重根
∴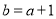 且
且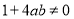 又 ∵
又 ∵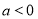 ∴
∴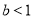 且
且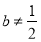 4分
4分
(2)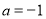 時
時 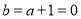 即方程
即方程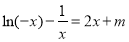 在
在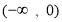 上有兩個不等實根
上有兩個不等實根
即方程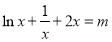 在
在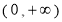 上有兩個不等實根
上有兩個不等實根
令
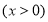
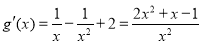
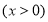
∴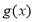 在
在 上單調遞減,在
上單調遞減,在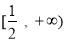 上單調遞增
上單調遞增 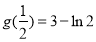
當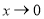 時,
時,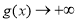 且當
且當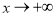 時,
時,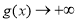
∴當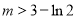 時,方程
時,方程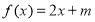 有兩個不相等的實數根 8分
有兩個不相等的實數根 8分
(3)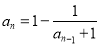 ∴
∴ 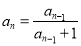 ∴
∴ 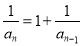 ∴
∴ 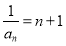
∴ 10分
10分
由(2)知
代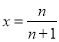 得
得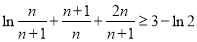 即
即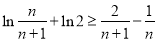
∴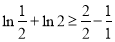
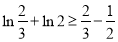

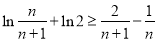
累加得
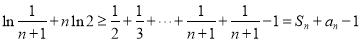
即 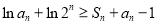 ∴
∴ 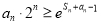 得證 14分
得證 14分
考點:函數的極值,函數的最值,數列的通項公式,數列求和,函數的單調性.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源:2013-2014學年江西省鷹潭市高三第二次模擬考試理科數學試卷(解析版) 題型:選擇題
設函數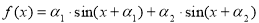 ,其中
,其中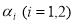 為已知實常數,
為已知實常數,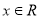 ,則下列命題中錯誤的是( )
,則下列命題中錯誤的是( )
A.若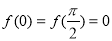 ,則
,則 對任意實數
對任意實數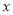 恒成立;
恒成立;
B.若 ,則函數
,則函數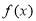 為奇函數;
為奇函數;
C.若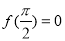 ,則函數
,則函數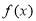 為偶函數;
為偶函數;
D.當 時,若
時,若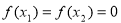 ,則
,則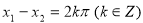 .
.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江西省盟校高三第二次聯考理科數學試卷(解析版) 題型:選擇題
已知點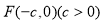 是雙曲線
是雙曲線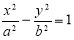 的左焦點,離心率為
的左焦點,離心率為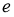 ,過
,過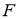 且平行于雙曲線漸近線的直線與圓
且平行于雙曲線漸近線的直線與圓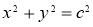 交于點
交于點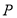 ,且點
,且點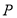 在拋物線
在拋物線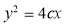 上,則
上,則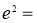 ( )
( )
A.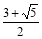 B.
B.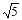 C.
C.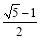 D.
D.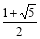
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江西省盟校高三第一次聯考理科數學試卷(解析版) 題型:解答題
設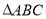 的內角
的內角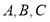 所對的邊分別為
所對的邊分別為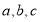 ,且有
,且有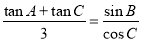 .
.
(1)求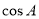 的值;
的值;
(2)若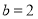 ,
,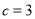 ,
, 為
為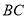 上一點.且
上一點.且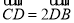 ,求
,求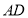 的長.
的長.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江西省盟校高三第一次聯考理科數學試卷(解析版) 題型:選擇題
如圖,已知正方體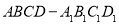 的棱長是1,點
的棱長是1,點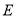 是對角線
是對角線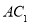 上一動點,記
上一動點,記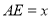 (
(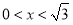 ),過點
),過點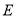 平行于平面
平行于平面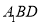 的截面將正方體分成兩部分,其中點
的截面將正方體分成兩部分,其中點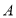 所在的部分的體積為
所在的部分的體積為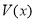 ,則函數
,則函數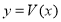 的圖像大致為( )
的圖像大致為( )



A B


C D
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江西省盟校高三第一次聯考文科數學試卷(解析版) 題型:填空題
已知直線 與圓
與圓 相交于
相交于 兩點,其中
兩點,其中 成等差數列,
成等差數列, 為坐標原點,則
為坐標原點,則 =___________.
=___________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江西省宜春市高三考前模擬文科數學試卷(解析版) 題型:解答題
在△ABC中,a、b、c分別為角A、B、C所對的邊,且
(2b+c)cosA+acosC =0
(1)求角A的大小:
(2)求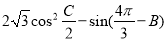 的最大值,并求取得最大值時角 B.C的大小.
的最大值,并求取得最大值時角 B.C的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com