
分析 (1)利用誘導公式,同角三角函數基本關系式化簡函數解析式,進而利用誘導公式,特殊角的三角函數值即可得解.
(2)由f(α )=-tanα=$\frac{2}{5}$,利用同角三角函數基本關系式可求cosα=±$\sqrt{\frac{1}{1+ta{n}^{2}α}}$的值.
解答 解:(1)f(α)=$\frac{sin(α-\frac{13π}{2})•tan(α-3π)}{cos(α+\frac{9π}{2})•tan(\frac{7π}{2}+α)}$=$\frac{(-cosα)tanα}{(-sinα)cotα}$=-tanα,
可得:f(-$\frac{67π}{6}$)=-tan(-$\frac{67π}{6}$)=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$.
(2)∵f(α )=-tanα=$\frac{2}{5}$,可求:tanα=-$\frac{2}{5}$,
∴cosα=±$\sqrt{\frac{1}{1+ta{n}^{2}α}}$=±$\sqrt{\frac{1}{1+\frac{4}{25}}}$=±$\frac{5\sqrt{29}}{29}$.
點評 本題主要考查了誘導公式,同角三角函數基本關系式,特殊角的三角函數值在三角函數化簡求值中的應用,考查了轉化思想,屬于基礎題.


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:解答題
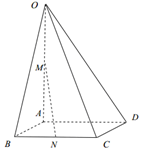 如圖,在四棱錐O-ABCD中,底面ABCD是四邊長為$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M為OA的中點,N為BC的中點.
如圖,在四棱錐O-ABCD中,底面ABCD是四邊長為$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M為OA的中點,N為BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2k-1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=-x2+2x+3,x∈[-1,2)
已知函數f(x)=-x2+2x+3,x∈[-1,2)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com