
分析 根據這種商品當天的市場價格與他的進貨量(件)加上20成反比,這種商品每件進價為2元.他進100件這種商品時,當天賣完,利潤為100元,求出比例系數,可得利潤函數,再換元,利用基本不等式,即可得出結論.
解答 解:由題意,設市場價格y元,他的進貨量為x件,則y=$\frac{k}{x+20}$,
∵這種商品每件進價為2元.他進100件這種商品時,當天賣完,利潤為100元,
∴100=($\frac{k}{120}$-2)×100,∴k=360,
∴利潤L=($\frac{360}{x+20}$-2)x,
設x+20=t(t≥20),則L=400-($\frac{7200}{t}$+2t)≤400-240=160,
當且僅當$\frac{7200}{t}$=2t,即t=60,x=40時,最大利潤是160元.
點評 本題考查利用數學知識解決實際問題,考查基本不等式的運用,正確求出函數的解析式是關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | f($\sqrt{2}$)>f(-$\sqrt{2}$) | B. | f(-2)>f(3) | C. | f(3)<f(4) | D. | f($\sqrt{2}$)>f($\sqrt{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
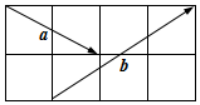 如圖,在2×4的方格紙中,若$\overrightarrow{a}$和$\overrightarrow{b}$是起點和終點均在格點的向量,則向量2$\overrightarrow a$+$\overrightarrow b$與$\overrightarrow a$-$\overrightarrow b$的夾角余弦值是$-\frac{{\sqrt{10}}}{10}$.
如圖,在2×4的方格紙中,若$\overrightarrow{a}$和$\overrightarrow{b}$是起點和終點均在格點的向量,則向量2$\overrightarrow a$+$\overrightarrow b$與$\overrightarrow a$-$\overrightarrow b$的夾角余弦值是$-\frac{{\sqrt{10}}}{10}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com