
| A. | $|{b-a+\frac{1}{c-b}}|≥2$ | B. | a3b+b3c+c3a≥a4+b4+c4 | ||
| C. | b2≥ac | D. | |b|-|a|≤|c|-|b| |
分析 本題是選擇題,可以采用特值法與排除法結合,不妨取a,b,c分別為1,2,3,不難選出答案B.
解答 解:對于選擇題,可以用特值法與排除法
設a=1,b=2,c=3
∴ab+bc+ca=11 a2+b2+c2=14
所以B不成立,故選B.
對于其他三個選項證明如下:
設等差數列的公差為d≠0
∴b-a=c-b=d∴|b-a+$\frac{1}{c-b}$|=|d+$\frac{1}p9vv5xb5$|≥2,故A正確,
∵a,b,c成等差數列
∴2b=a+c≥2$\sqrt{ac}$,
∴b2≥ac,故C正確,
又|2b|=|a+c|≤|a|+|c|
∴|b|-|a|≤|c|-|b|,故D正確,
故選:B.
點評 本題旨在考查不等關系與不等式以及等差數列的性質,但本題是選擇題,用特值法與排除法解決應該是應試的技巧,值得注意.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
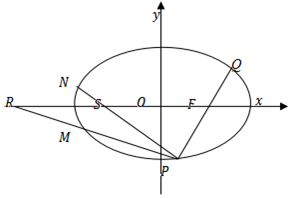 如圖,橢圓C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦點為F,P為橢圓上一動點,連接PF交橢圓于Q點,且|PQ|的最小值為$\frac{8}{3}$.
如圖,橢圓C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦點為F,P為橢圓上一動點,連接PF交橢圓于Q點,且|PQ|的最小值為$\frac{8}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com