
分析 由題意知本題是一個古典概型,試驗發生包含的事件數是36,求出滿足條件的事件是直線ax+by=0與圓(x-2)2+y2=2無公共點的基本事件個數,代入古典概型概率公式得到結果.
解答 解:將一枚骰子先后拋擲兩次得到的點數依次記為a,b,基本事件總數是36種,
∵直線ax+by=0與圓(x-2)2+y2=2無公共點,則有 $\frac{|2a|}{\sqrt{{a}^{2}{+b}^{2}}}$>$\sqrt{2}$⇒a>b,
∴滿足該條件的基本事件有15種,
故所求概率為P=$\frac{15}{36}$=$\frac{5}{12}$.
故答案為:$\frac{5}{12}$.
點評 本題考查古典概型,考查對立事件的概率,考查簡單直線與圓的位置關系,是一個綜合題,本題解題的難點不是古典概型,而是題目中出現的其他的知識點.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
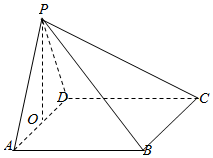 如圖,在四棱錐P-ABCD中,底面ABCD是邊長為2的正方形,側面PAD是正三角形,且平面PAD⊥平面ABCD,O為棱AD的中點.
如圖,在四棱錐P-ABCD中,底面ABCD是邊長為2的正方形,側面PAD是正三角形,且平面PAD⊥平面ABCD,O為棱AD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $|{b-a+\frac{1}{c-b}}|≥2$ | B. | a3b+b3c+c3a≥a4+b4+c4 | ||
| C. | b2≥ac | D. | |b|-|a|≤|c|-|b| |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com