
分析 (1)化簡函數f(x)為正弦型函數,根據正弦函數的單調性求出f(x)的單調減區間;
(2)利用正弦定理求出A的取值范圍,再求f(A)的取值范圍即可.
解答 解:(1)$f(x)=\frac{1}{2}-{cos^2}x+\sqrt{3}sinxcosx$
=$\frac{1}{2}$-$\frac{1+cos2x}{2}$+$\frac{\sqrt{3}}{2}$sin2x
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x
=sin(2x-$\frac{π}{6}$),
令$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,k∈Z,
解得$\frac{π}{3}$+kπ≤x≤$\frac{5π}{6}$+kπ,k∈Z;
∴f(x)的單調遞減區間是$[\frac{π}{3}+kπ,\frac{5π}{6}+kπ],k∈Z$;…(6分)
(2)△ABC中,滿足sin2B+sin2C>sinBsinC+sin2A,
∴b2+c2>bc+a2,
即b2+c2-a2>bc,
∴cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$>$\frac{1}{2}$,
∴0<A<$\frac{π}{3}$;
∴-$\frac{π}{6}$<2A-$\frac{π}{6}$<$\frac{π}{2}$,
∴-$\frac{1}{2}$<sin(2A-$\frac{π}{6}$)<1,
∴f(A)的取值范圍是(-$\frac{1}{2}$,1).…(12分)
點評 本題考查了三角函數的化簡以及正弦定理的應用問題,是基礎題目.


科目:高中數學 來源: 題型:填空題
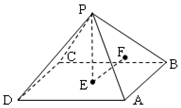 如圖,P-ABCD是棱長均為1的正四棱錐,頂點P在平面ABCD內的正投影為點E,點E在平面PAB內的正投影為點F,則 tan∠PEF=$\sqrt{2}$.
如圖,P-ABCD是棱長均為1的正四棱錐,頂點P在平面ABCD內的正投影為點E,點E在平面PAB內的正投影為點F,則 tan∠PEF=$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | A∩B=∅ | B. | ∁AB=B | C. | A⊆B | D. | B$\begin{array}{l}?\\≠\end{array}$A |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x-y+2=0 | B. | x+y-2=0 | C. | x-y-2=0 | D. | x+y+2=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[\frac{ln3}{3},\frac{1}{e})$ | B. | $[\frac{ln3}{3},\frac{1}{2e})$ | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{1}{2e})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
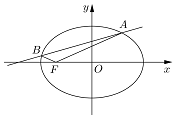 已知橢圓C以原點為中心,左焦點F的坐標是(-1,0),長軸長是短軸長的$\sqrt{2}$倍,直線l與橢圓C交于點A與B,且A、B都在x軸上方,滿足∠OFA+∠OFB=180°;
已知橢圓C以原點為中心,左焦點F的坐標是(-1,0),長軸長是短軸長的$\sqrt{2}$倍,直線l與橢圓C交于點A與B,且A、B都在x軸上方,滿足∠OFA+∠OFB=180°;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com