
 如圖,點(diǎn)E是菱形ABCD所在平面外一點(diǎn),EA⊥平面ABCD,EA∥FB∥GD,∠ABC=60°,EA=AB=2BF=2GD.
如圖,點(diǎn)E是菱形ABCD所在平面外一點(diǎn),EA⊥平面ABCD,EA∥FB∥GD,∠ABC=60°,EA=AB=2BF=2GD.分析 (I)連結(jié)BD交AC于O,取EC的中點(diǎn)M,連結(jié)OM,GM,建立空間坐標(biāo)系,利用向量證明GM⊥AE,GM⊥AC可得GM⊥平面EAC,于是平面平面EAC⊥平面ECG;
(II)求出平面EBC和平面BCF的法向量,計(jì)算兩法向量的夾角即可得出二面角的大小.
解答  (I)證明:連結(jié)BD交AC于O,取EC的中點(diǎn)M,連結(jié)OM,GM,
(I)證明:連結(jié)BD交AC于O,取EC的中點(diǎn)M,連結(jié)OM,GM,
∵O,M分別是AC,EC的中點(diǎn),
∴OM∥EA,又∵EA⊥平面ABCD,
∴OM⊥平面ABCD,
以O(shè)為原點(diǎn),以O(shè)B,OC,OM為坐標(biāo)軸建立空間坐標(biāo)系如圖所示:
設(shè)BF=1,則A(0,-1,0),C(0,1,0),E(0,-1,2),D(-$\sqrt{3}$,0,0),
G(-$\sqrt{3}$,0,1),M(0,0,1),
∴$\overrightarrow{AC}$=(0,2,0),$\overrightarrow{AE}$=(0,0,2),$\overrightarrow{GM}$=($\sqrt{3}$,0,0),
∴$\overrightarrow{GM}•\overrightarrow{AC}$=0,$\overrightarrow{GM}•\overrightarrow{AE}$=0,
∴GM⊥AC,GM⊥AE,又AE∩AC=A,
∴GM⊥平面EAC,又GM?平面ECG,
∴平面EAC⊥平面ECG.
(II)解:B($\sqrt{3}$,0,0),F(xiàn)($\sqrt{3}$,0,1),
∴$\overrightarrow{EC}$=(0,2,-2),$\overrightarrow{EB}$=($\sqrt{3}$,1,-2),$\overrightarrow{EF}$=($\sqrt{3}$,1,-1),
設(shè)平面BEC的法向量為$\overrightarrow{m}$=(x1,y1,z1),平面FEC的法向量為$\overrightarrow{n}$=(x2,y2,z2),
則$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{EC}=0}\\{\overrightarrow{m}•\overrightarrow{EB}=0}\end{array}\right.$,$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EC}=0}\\{\overrightarrow{n}•\overrightarrow{EF}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2{y}_{1}-2{z}_{1}=0}\\{\sqrt{3}{x}_{1}+{y}_{1}-2{z}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{2{y}_{2}-2{z}_{2}=0}\\{\sqrt{3}{x}_{2}+{y}_{2}-{z}_{2}=0}\end{array}\right.$,
令x1=$\sqrt{3}$得$\overrightarrow{m}$=($\sqrt{3}$,3,3),令y2=1得$\overrightarrow{n}$=(0,1,1).
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{6}{\sqrt{21}•\sqrt{2}}$=$\frac{\sqrt{42}}{7}$.
∴二面角B-PC-F的余弦值為$\frac{\sqrt{42}}{7}$.
點(diǎn)評(píng) 本題考查了面面垂直的判定,空間向量在立體幾何中的應(yīng)用,空間角的計(jì)算,屬于中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 當(dāng)a>1時(shí),函數(shù)y=ax是增函數(shù),因?yàn)?>1,所以函數(shù)y=2x是增函數(shù),這種推理是合情推理 | |
| B. | 在平面中,對于三條不同的直線a,b,c,若a∥b,b∥c,則a∥c,將此結(jié)論放到空間中也是如此.這種推理是演繹推理 | |
| C. | 命題$P:?{x_0}∈R,{e^{x_0}}<{x_0}$的否定是¬P:?x∈R,ex>x | |
| D. | 若分類變量X與Y的隨機(jī)變量K2的觀測值k越小,則兩個(gè)分類變量有關(guān)系的把握性越小 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
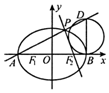 已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{1}{2}$,左、右焦點(diǎn)為F1,F(xiàn)2,點(diǎn)M為橢圓C上的任意一點(diǎn),$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值為2.
已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{1}{2}$,左、右焦點(diǎn)為F1,F(xiàn)2,點(diǎn)M為橢圓C上的任意一點(diǎn),$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值為2.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $±\frac{3}{5}$ | D. | $±\frac{4}{5}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com