Question

4．定義在[0，+∞）上的函數f（x）滿足：①當x∈[1，2）時，$f（x）=\frac{1}{2}-|{x-\frac{3}{2}}|$；②?x∈[0，+∞）都有f（2x）=2f（x）．設關于x的函數F（x）=f（x）-a的零點從小到大依次為x₁，x₂，x₃，…x_n，…，若$a∈（{\frac{1}{2}，1}）$，則x₁+x₂+…+x_2n=6×（2ⁿ-1）．

Answer 1

分析 利用已知當x∈[1，2）時，$f（x）=\frac{1}{2}-|{x-\frac{3}{2}}|$；?x∈[0，+∞）都有f（2x）=2f（x）．可得當x∈[2，4）時的解析式，同理，當x∈[4，8）時，f（x）的解析式，分別作出y=f（x），y=a，則F（x）=f（x）-a在區(qū)間（2，3）和（3，4）上各有一個零點，分別為x₁，x₂，且滿足x₁+x₂=2×3，依此類推：x₃+x₄=2×6，…，x₂₀₁₃+x₂₀₁₄=2×3×2^n-1．利用等比數列的前n項和公式即可得出．

解答 解：∵①當x∈[1，2）時，$f（x）=\frac{1}{2}-|{x-\frac{3}{2}}|$；②?x∈[0，+∞）都有f（2x）=2f（x）．
當x∈[2，4）時，$\frac{1}{2}x$∈[1，2），
f（x）=2f（$\frac{1}{2}$x）=2（$\frac{1}{2}$-|$\frac{1}{2}x$-$\frac{3}{2}$|）=1-|x-3|，x∈[4，8）時，$\frac{1}{2}x$∈[2，4），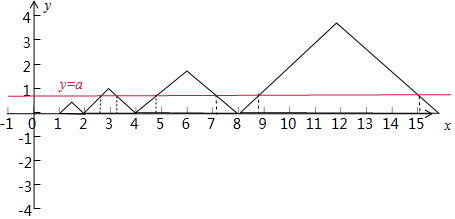
f（x）=2f（$\frac{1}{2}$x）=2（1-|$\frac{1}{2}$x-3|）=2-|x-6|，
同理，則$a∈（{\frac{1}{2}，1}）$，F（x）=f（x）-a在區(qū)間（2，3）和（3，4）上各有1個零點，分別為x₁，x₂，且滿足x₁+x₂=2×3=6，
依此類推：x₃+x₄=2×6=12，x₅+x₆=2×12=24…，x_2n-1+x_2n=2×3×2^n-1．
∴當$a∈（{\frac{1}{2}，1}）$時，x₁+x₂+…+x_2n-1+x_2n=6×（1+2+2²+…+2^n-1）=6×$\frac{1（1-{2}^{n}）}{1-2}$=6×（2ⁿ-1），
故答案為：6×（2ⁿ-1）．

點評 本題考查了函數的圖象與性質、區(qū)間轉換、對稱性、等比數列的前n項和公式等基礎知識與基本技能，屬于難題．