
分析 由新定義可得f(x)為奇函數且為減函數,則稱函數f(x)為“理想函數”.運用奇偶性的定義和二次函數和反比例函數,以及對數函數的單調性,即可判斷.
解答 解:對照新定義可得,函數為奇函數且為減函數,才為“理想函數”.
①$f(x)=\frac{1}{x}$滿足f(-x)+f(x)=0,但f(x)在定義域{x|x≠0}不為減函數,則函數f(x)不為“理想函數”;
②f(x)=x2滿足f(-x)=f(x),即f(x)為偶函數,則函數f(x)不為“理想函數”;
③$f(x)=\left\{\begin{array}{l}-{x^2}(x≥0)\\{x^2}(x<0)\end{array}\right.$,當x=0時,f(0)=0;當x>0時,-x<0,f(-x)=(-x)2=-f(x);同樣x<0時,也有f(-x)=-f(x),
綜上可得f(x)為奇函數;當x<0時,f(x)遞減;當x>0時,f(x)也遞減;且f(x)連續,故f(x)為“理想函數”;
④$f(x)={log_{\frac{1}{2}}}(\sqrt{{x^2}+1}+x)$,由x+$\sqrt{1+{x}^{2}}$>0,當x≥0時,顯然成立;當x<0時,$\sqrt{1+{x}^{2}}$>-x,
平方可得1+x2>x2成立,則定義域為R,f(-x)+f(x)=log${\;}_{\frac{1}{2}}$(-x+$\sqrt{1+{x}^{2}}$)+log${\;}_{\frac{1}{2}}$(x+$\sqrt{1+{x}^{2}}$)=log${\;}_{\frac{1}{2}}$(x2+1-x2)=0,
則f(x)為奇函數;又x>0時,x+$\sqrt{1+{x}^{2}}$為遞增函數,由復合函數的性質:同增異減,可得f(x)為減函數,
則f(x)為“理想函數”.
故答案為:③④.
點評 本題考查新定義的理解和運用,主要考查函數的奇偶性和單調性,注意運用定義法是解題的關鍵,屬于中檔題.


科目:高中數學 來源: 題型:解答題
 已知集合 A={x|x2-5x-6<0},集合 B={x|6x2-5x+1≥0},集合C={x|(x-m)(x-m-9)<0}.
已知集合 A={x|x2-5x-6<0},集合 B={x|6x2-5x+1≥0},集合C={x|(x-m)(x-m-9)<0}.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{36}$ | D. | $\frac{25}{36}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第二象限角或第三象限的角 | B. | 第一象限角或第四象限的角 | ||
| C. | 第三象限角或第四象限的角 | D. | 終邊在直線y=-x左下方的角 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
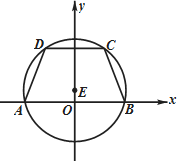 如圖所示,等腰梯形ABCD的底邊AB在x軸上,頂點A與頂點B關于原點O對稱,且底邊AB和CD的長分別為6和$2\sqrt{6}$,高為3.
如圖所示,等腰梯形ABCD的底邊AB在x軸上,頂點A與頂點B關于原點O對稱,且底邊AB和CD的長分別為6和$2\sqrt{6}$,高為3.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com