已知|
|=6，|
|=4，
與
的夾角為120°，則（
+2
）•（
-3
）的值是（ ）
考點：平面向量數(shù)量積的運算
專題：平面向量及應(yīng)用
分析：利用向量的乘法展開所求，利用已知可求向量的數(shù)量積以及模．
解答：
解：由已知可得
•=||||cos120°=-6×4×
=-12，
所以（
+2
）•（
-3
）=
2-62-•=36-96+12=-48；
故選C．
點評：本題考查了向量的運算，數(shù)量積的乘法，模與向量的平方等知識點，屬于基礎(chǔ)題．
練習(xí)冊系列答案
相關(guān)習(xí)題
科目：高中數(shù)學(xué)
來源：
題型：
已知點 A（0，2）為圓M：x
2+y
2-2ax-2ay=0外一點，圓M上存在點T使得∠MAT=45°，則實數(shù)a的取值范圍是
．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知函數(shù)f（x）=x-2m2+m+3（m∈Z）為偶函數(shù)，且f（3）＜f（5）
（1）求m的值，并確定f（x）的解析式．
（2）若y=loga[f（x）-ax]（a＞0，且a≠1）在區(qū)間[2，3]上為增函數(shù)，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
設(shè)f（x）是定義在R上的奇函數(shù)且對任意實數(shù)x，恒有f（x+2）=-f（x），當(dāng)x∈[0，2]時，f（x）=2x-x2．
（1）求證：f（x）的周期函數(shù)；
（2）x∈[2，4]，求f（x）的解析式；
（3）計算f（0）+f（1）+f（2）+…+f（2013）的值．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
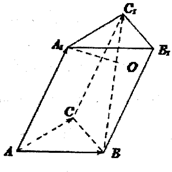
如圖所示，三棱柱ABC-A
1B
1C
1中，AA
1=2AB=2AC=2．∠A
1AB=∠A
1AC=∠BAC=60°，設(shè)
=
，
=
，
=
．
（1）試用向量
，
，
表示
，并求|
|；
（2）在平行四邊形BB
1C
1C內(nèi)是否存在一點O，使得A
1O⊥平面BB
1C
1C，若不存在，請說明理由；若存在，試確定O點的位置．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
下列四個語句中，有一個語句是錯誤的，這個錯誤的語句序號為．
①若
-
=
，則
=
②若
•
=0，則
=
或
=
③若k∈R，k
=
，則k=0或
=
．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知f（x）=
，命題p：“?x∈[-1，0）∪（0，1]，f（x）≥ax”，且命題￢p為假命題，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
若不等式1+2
x+4
xa＞0在x∈（-∞，-1]時總成立，求實數(shù)a的取值范圍
．
查看答案和解析>>
