
分析 (1)集合M表示的區域的面積為6×4=24,此圓x2+y2=4的面積表示滿足條件的基本事件,所求為面積比;
(2)求出滿足以(x,y)為坐標的點到直線x+y=0的距離不大于$\sqrt{2}$面積,則求面積比即可.
解答  解:(1)A=[-3,3],B=[-2,2],設M={(x,y)|x∈A,y∈B},表示的區域的面積為6×4=24.
解:(1)A=[-3,3],B=[-2,2],設M={(x,y)|x∈A,y∈B},表示的區域的面積為6×4=24.
圓x2+y2=4的面積為4π,
∴以(x,y)為坐標的點落在圓x2+y2=4內的概率為P1=$\frac{4π}{24}$=$\frac{π}{6}$,
(2)由題意,到直線x+y=0的距離不大于$\sqrt{2}$的點為夾在兩條平行直線x+y-2=0與x+y+2=0之間的范圍內,如圖所示,
故所求事件的概率為${P_2}=\frac{{6×4-2×\frac{1}{2}×3×3}}{6×4}=\frac{5}{8}$.
點評 本題考查了幾何概型的概率求法,關鍵是將所求的概率利用基本事件的集合度量即區域的長度或者面積或者體積表示,求比值.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
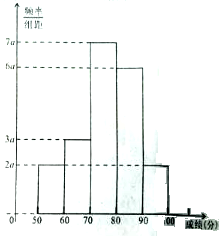 20名學生某次數學考試成績(單位:分)的頻率分布直方圖如圖.
20名學生某次數學考試成績(單位:分)的頻率分布直方圖如圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 甲、乙、丙.丁四輛玩具賽車同時從起點出發并做勻速直線運動,丙車最先到達終點.丁車最后到達終點.若甲、乙兩車的s-t圖象如圖所示,則對于丙、丁兩車的圖象所在區域,判斷正確的是( )
甲、乙、丙.丁四輛玩具賽車同時從起點出發并做勻速直線運動,丙車最先到達終點.丁車最后到達終點.若甲、乙兩車的s-t圖象如圖所示,則對于丙、丁兩車的圖象所在區域,判斷正確的是( )| A. | 丙在Ⅲ區域,丁在Ⅰ區域 | B. | 丙在Ⅰ區城,丁在Ⅲ區域 | ||
| C. | 丙在Ⅱ區域,丁在Ⅰ區域 | D. | 丙在Ⅲ區域,丁在Ⅱ區域 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
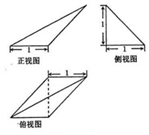
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com