
(本題滿分14分)已知圓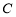 :
: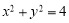 .
.
(Ⅰ)直線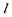 過點
過點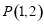 ,且與圓
,且與圓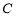 交于
交于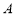 、
、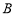 兩點,若
兩點,若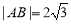 ,求直線
,求直線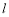 的方程;
的方程;
(Ⅱ)過圓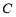 上一動點
上一動點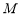 作平行于
作平行于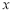 軸的直線
軸的直線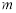 ,設
,設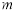 與
與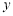 軸的交點為
軸的交點為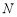 ,若向量
,若向量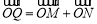 ,求動點
,求動點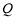 的軌跡方程,并說明此軌跡是什么曲線.
的軌跡方程,并說明此軌跡是什么曲線.
(Ⅰ)x=1,3x-4y+5=0,;
(Ⅱ)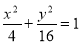 (y≠0)軌跡為長軸長為8,短軸長為4,焦距為4
(y≠0)軌跡為長軸長為8,短軸長為4,焦距為4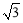 且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
【解析】
試題分析:(Ⅰ)由直線與圓位置關系得:半徑,半弦長,圓心到直線距離構成勾股,即 ,因此d=1,又直線
,因此d=1,又直線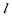 過點
過點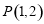 ,故利用直線方程點斜式求解,注意先討論斜率不存在情況:若
,故利用直線方程點斜式求解,注意先討論斜率不存在情況:若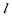 ⊥x軸,直線方程為x=1,A(1,-
⊥x軸,直線方程為x=1,A(1,-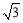 ),B(1,
),B(1,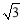 ),
),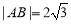 ,適合;若
,適合;若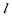 的斜率存在,設
的斜率存在,設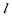 的方程為y=k(x-1)+2,圓心到直線的距離為d=1=
的方程為y=k(x-1)+2,圓心到直線的距離為d=1= 解得k=
解得k=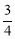 ,直線方程為3x-4y+5=0,(Ⅱ)相關點法求軌跡方程:先找出所求的與已知動點之間關系,代入已知動點軌跡,化簡即得所求動點軌跡方程:設M(
,直線方程為3x-4y+5=0,(Ⅱ)相關點法求軌跡方程:先找出所求的與已知動點之間關系,代入已知動點軌跡,化簡即得所求動點軌跡方程:設M(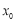 ,
,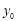 )(
)(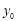 ≠0).則N(0,
≠0).則N(0,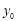 ),Q(x,y),則
),Q(x,y),則  ,又
,又 ,動點Q的軌跡方程為
,動點Q的軌跡方程為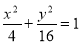 (y≠0)軌跡為長軸長為8,短軸長為4,焦距為4
(y≠0)軌跡為長軸長為8,短軸長為4,焦距為4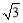 且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
試題解析:【解析】
(Ⅰ)若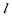 ⊥x軸,直線方程為x=1,A(1,-
⊥x軸,直線方程為x=1,A(1,-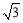 ),B(1,
),B(1,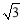 ),
),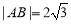 ,適合---3分
,適合---3分
若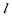 的斜率存在,設
的斜率存在,設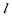 的方程為y=k(x-1)+2,圓心到直線的距離為d=
的方程為y=k(x-1)+2,圓心到直線的距離為d= ,圓半徑為2,故
,圓半徑為2,故 ,k=
,k=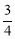 ,直線方程為3x-4y+5=0, ------7分
,直線方程為3x-4y+5=0, ------7分
綜上所求直線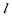 的方程為x=1,3x-4y+5=0,; -----8分
的方程為x=1,3x-4y+5=0,; -----8分
(Ⅱ)設M(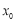 ,
,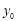 )(
)(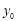 ≠0).則N(0,
≠0).則N(0,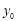 ),Q(x,y),則
),Q(x,y),則  ----2分
----2分
又 ,動點Q的軌跡方程為
,動點Q的軌跡方程為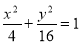 (y≠0) -----5分
(y≠0) -----5分
軌跡為長軸長為8,短軸長為4,焦距為4 且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點.----6分
且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點.----6分
考點:直線與圓位置關系,軌跡方程


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2014-2015學年江蘇省等五校高三12月第一次聯考文科數學試卷(解析版) 題型:解答題
某單位有員工1000名,平均每人每年創造利潤10萬元.為了增加企業競爭力,決定優化產業結構,調整出x (x∈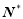 )名員工從事第三產業,調整后他們平均每人每年創造利潤為
)名員工從事第三產業,調整后他們平均每人每年創造利潤為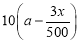 萬元(a>0),剩下的員工平均每人每年創造的利潤可以提高0.2x%.
萬元(a>0),剩下的員工平均每人每年創造的利潤可以提高0.2x%.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整出多少名員工從事第三產業?
(2)在(1)的條件下,若調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,則a的取值范圍是多少?
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇教育學院附屬高中高三上學期期中理科數學試卷(解析版) 題型:解答題
選修4-4:坐標系與參數方程
已知曲線 的參數方程為
的參數方程為 ,曲線
,曲線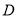 的極坐標方程為
的極坐標方程為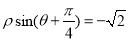 .
.
(1)將曲線 的參數方程化為普通方程;
的參數方程化為普通方程;
(2)曲線 與曲線
與曲線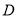 有無公共點?試說明理由.
有無公共點?試說明理由.
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇教育學院附屬高中高三上學期期中理科數學試卷(解析版) 題型:填空題
給出以下四個命題:
①已知命題 ;命題
;命題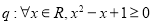 .則命題
.則命題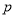 和
和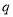 都是真命題;
都是真命題;
②過點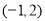 且在
且在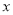 軸和
軸和 軸上的截距相等的直線方程是
軸上的截距相等的直線方程是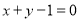 ;
;
③函數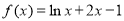 在定義域內有且只有一個零點;
在定義域內有且只有一個零點;
④先將函數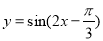 的圖像向右平移
的圖像向右平移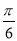 個單位,再將新函數的周期擴大為原來的兩倍,則所得圖像的函數解析式為
個單位,再將新函數的周期擴大為原來的兩倍,則所得圖像的函數解析式為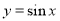 .
.
其中正確命題的序號為 .(把你認為正確的命題序號都填上)
查看答案和解析>>
科目:高中數學 來源:2014-2015學年浙江省嘉興市高三新高考單科綜合調研三文科數學試卷(解析版) 題型:選擇題
函數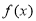 的定義域為
的定義域為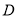 ,若滿足:
,若滿足:
① 在
在 內是單調函數;
內是單調函數;
②存在 ,使
,使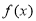 在
在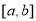 上的值域為
上的值域為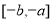 ,那么
,那么 叫做對稱函數.
叫做對稱函數.
現有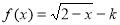 是對稱函數,那么
是對稱函數,那么 的取值范圍是( )
的取值范圍是( )
A.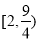 B.
B.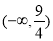 C.
C.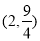 D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com