
【題目】已知![]() 是定義在
是定義在![]() 上的函數,如果存在常數
上的函數,如果存在常數![]() ,對區間
,對區間![]() 的任意劃分:
的任意劃分:![]() ,和式
,和式![]() 恒成立,則稱
恒成立,則稱![]() 為
為![]() 上的“絕對差有界函數”。注:
上的“絕對差有界函數”。注:![]() 。
。
(1)證明函數![]() 在
在![]() 上是“絕對差有界函數”。
上是“絕對差有界函數”。
(2)證明函數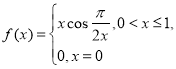 不是
不是![]() 上的“絕對差有界函數”。
上的“絕對差有界函數”。
(3)記集合![]() 存在常數
存在常數![]() ,對任意的
,對任意的![]() ,有
,有![]() 成立
成立![]() ,證明集合
,證明集合![]() 中的任意函數
中的任意函數![]() 為“絕對差有界函數”,并判斷
為“絕對差有界函數”,并判斷![]() 是否在集合
是否在集合![]() 中,如果在,請證明并求
中,如果在,請證明并求![]() 的最小值;如果不在,請說明理由。
的最小值;如果不在,請說明理由。
【答案】(1)詳見解析;(2)詳見解析;(3)證明詳見解析,![]() 的最小值為
的最小值為![]() .
.
【解析】
(1)首先化簡函數![]() ,并且函數在區間
,并且函數在區間![]() 上為單調遞增函數,由定義可知任意劃分區間
上為單調遞增函數,由定義可知任意劃分區間![]() ,根據定義求
,根據定義求![]() ;
;
(2)取區間![]() 的一個劃分:
的一個劃分:![]() ,代入則有
,代入則有![]() ,由此根據定義判斷是否存在
,由此根據定義判斷是否存在![]() ;
;
(3)利用不等式的傳遞性證明![]() ,
,
![]() ,利用和差化積公式化簡證明求
,利用和差化積公式化簡證明求![]() 的最小值.
的最小值.
解:(1)因為![]() 在區間
在區間![]() 上為單調遞增函數,
上為單調遞增函數,
所以當![]() 時,有
時,有![]() ,
,
所以![]() 。
。
從而對區間![]() 的任意劃分:
的任意劃分:![]() ,存在
,存在![]() ,
,![]() 成立。
成立。
綜上,函數![]() 在
在![]() 上是“絕對差有界函數”。
上是“絕對差有界函數”。
(2)取區間![]() 的一個劃分:
的一個劃分:![]() ,
,
則有:
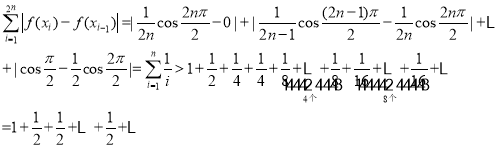
所以對任意常數![]() ,只要
,只要![]() 足夠大,就有區間
足夠大,就有區間![]() 的一個劃分:
的一個劃分:
![]() 滿足
滿足![]() 。
。
(3)證明:任取![]() ,存在常數
,存在常數![]() 有
有![]() 成立。從而對區間
成立。從而對區間![]() 的任意劃分:
的任意劃分:![]() ,和式
,和式![]() 成立。取
成立。取![]() ,所以集合
,所以集合![]() 中的任意函數
中的任意函數![]() 為“絕對差有界函數”。
為“絕對差有界函數”。
因為![]() ,所以對任意的
,所以對任意的![]() 有
有
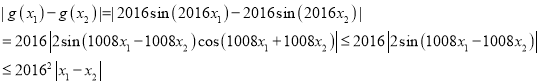 ,
,
所以![]() 的最小值為
的最小值為![]() 。
。


 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】設單調函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,如果單調函數
,如果單調函數![]() 使得函數
使得函數![]() 的值域也是
的值域也是![]() ,則稱函數
,則稱函數![]() 是函數
是函數![]() 的一個“保值域函數”.已知定義域為
的一個“保值域函數”.已知定義域為![]() 的函數
的函數![]() ,函數
,函數![]() 與
與![]() 互為反函數,且
互為反函數,且![]() 是
是![]() 的一個“保值域函數”,
的一個“保值域函數”,![]() 是
是![]() 的一個“保值域函數”,則
的一個“保值域函數”,則![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的上界.
的上界.
(1)設![]() ,判斷
,判斷![]() 在
在![]() 上是否為有界函數,若是,請說明理由,并寫出
上是否為有界函數,若是,請說明理由,并寫出![]() 的所有上界
的所有上界![]() 的集合;若不是,也請說明理由;
的集合;若不是,也請說明理由;
(2)若函數![]() 在
在![]() 上是以
上是以![]() 為上界的有界函數,求實數
為上界的有界函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2019年女排世界杯中,中國女子排球隊以11連勝的優異戰績成功奪冠,為祖國母親七十華誕獻上了一份厚禮.排球比賽采用5局3勝制,前4局比賽采用25分制,每個隊只有贏得至少25分,并同時超過對方2分時,才勝1局;在決勝局(第五局)采用15分制,每個隊只有贏得至少15分,并領先對方2分為勝.在每局比賽中,發球方贏得此球后可得1分,并獲得下一球的發球權,否則交換發球權,并且對方得1分.現有甲乙兩隊進行排球比賽:
(1)若前三局比賽中甲已經贏兩局,乙贏一局.接下來兩隊贏得每局比賽的概率均為![]() ,求甲隊最后贏得整場比賽的概率;
,求甲隊最后贏得整場比賽的概率;
(2)若前四局比賽中甲、乙兩隊已經各贏兩局比賽.在決勝局(第五局)中,兩隊當前的得分為甲、乙各14分,且甲已獲得下一發球權.若甲發球時甲贏1分的概率為![]() ,乙發球時甲贏1分的概率為
,乙發球時甲贏1分的概率為![]() ,得分者獲得下一個球的發球權.設兩隊打了
,得分者獲得下一個球的發球權.設兩隊打了![]() 個球后甲贏得整場比賽,求x的取值及相應的概率p(x).
個球后甲贏得整場比賽,求x的取值及相應的概率p(x).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點,若
的中點,若![]() 為線段
為線段![]() 上的動點(不含
上的動點(不含![]() ).
).
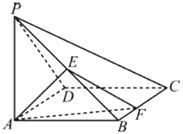
(1)平面![]() 與平面
與平面![]() 是否互相垂直?如果是,請證明;如果不是,請說明理由;
是否互相垂直?如果是,請證明;如果不是,請說明理由;
(2)求二面角![]() 的余弦值的取值范圍.
的余弦值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() 且側棱
且側棱![]() 其中
其中![]() 為
為![]() 的
的![]() 交點.
交點.
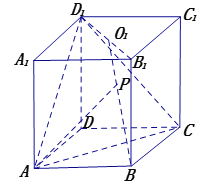
(1)求點![]() 到平面
到平面![]() 的距離;
的距離;
(2)在線段![]() 上,是否存在一個點
上,是否存在一個點![]() ,使得直線
,使得直線![]() 與
與![]() 垂直?若存在,求出線段
垂直?若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知非空集合![]() 是由一些函數組成,滿足如下性質:①對任意
是由一些函數組成,滿足如下性質:①對任意![]() ,
,![]() 均存在反函數
均存在反函數![]() ,且
,且![]() ;②對任意
;②對任意![]() ,方程
,方程![]() 均有解;③對任意
均有解;③對任意![]() 、
、![]() ,若函數
,若函數![]() 為定義在
為定義在![]() 上的一次函數,則
上的一次函數,則![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求證:函數
中,求證:函數![]() ;
;
(2)若函數![]() (
(![]() )在集合
)在集合![]() 中,求實數
中,求實數![]() 的取值范圍;
的取值范圍;
(3)若集合![]() 中的函數均為定義在
中的函數均為定義在![]() 上的一次函數,求證:存在一個實數
上的一次函數,求證:存在一個實數![]() ,使得對一切
,使得對一切![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個不相等的非零向量![]() ,兩組向量
,兩組向量![]() 和
和![]() 均由2個
均由2個![]() 和3個
和3個![]() 排列而成,記
排列而成,記![]() ,
,![]() 表示
表示![]() 所有可能取值中的最小值,則下列命題中
所有可能取值中的最小值,則下列命題中
(1)![]() 有5個不同的值;(2)若
有5個不同的值;(2)若![]() 則
則![]() 與
與![]() 無關;(3)若
無關;(3)若![]() ,則
,則![]() 與
與![]() 無關;(4)若
無關;(4)若![]() ,則
,則![]() ;(5)若
;(5)若![]() ,
,![]() ,則
,則![]() 與
與![]() 的夾角為
的夾角為![]() .正確的是( )
.正確的是( )
A.(1)(2)B.(2)(4)C.(3)(5)D.(1)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,
,![]() ,若
,若![]() -
-![]()
![]() …,則稱
…,則稱![]() 是
是![]() 的“收縮數列”.其中,
的“收縮數列”.其中,![]() ,
,![]() 分別表示
分別表示![]() 中的最大數和最小數.已知
中的最大數和最小數.已知![]() 為無窮數列,其前
為無窮數列,其前![]() 項和為
項和為![]() ,數列
,數列![]() 是
是![]() 的“收縮數列”.
的“收縮數列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 項和;
項和;
(2)證明:![]() 的“收縮數列”仍是
的“收縮數列”仍是![]() ;
;
(3)若![]() ,求所有滿足該條件的
,求所有滿足該條件的![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com