
| A. | 2 | B. | $-\sqrt{3}$ | C. | -2 | D. | 3 |
分析 設A((x1,y1),B(x2,y2),D(x0,y0),則x1+x2=2x0,y1+y2=2y0,由$\frac{{{x}_{1}}^{2}}{4}-\frac{{{y}_{1}}^{2}}{2}=1$,$\frac{{{x}_{2}}^{2}}{4}-\frac{{{y}_{2}}^{2}}{2}=1$得$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{4}=\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{2}$,即可得$\frac{{x}_{1}-{x}_{2}}{{y}_{1}-{y}_{2}}=2×\frac{2{y}_{0}}{2{x}_{0}}=2\frac{{y}_{0}}{{x}_{0}}$,$\frac{1}{{k}_{AB}}=2{k}_{OD}$.同理可得$\frac{1}{{k}_{BC}}=2{k}_{OE},\frac{1}{{k}_{AC}}=2{k}_{OF}$.即可.
解答 解:設A((x1,y1),B(x2,y2),D(x0,y0),則x1+x2=2x0,y1+y2=2y0.
由$\frac{{{x}_{1}}^{2}}{4}-\frac{{{y}_{1}}^{2}}{2}=1$,$\frac{{{x}_{2}}^{2}}{4}-\frac{{{y}_{2}}^{2}}{2}=1$得$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{4}=\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{2}$,
∴$\frac{{x}_{1}-{x}_{2}}{{y}_{1}-{y}_{2}}=2×\frac{2{y}_{0}}{2{x}_{0}}=2\frac{{y}_{0}}{{x}_{0}}$,∴$\frac{1}{{k}_{AB}}=2{k}_{OD}$.
同理可得$\frac{1}{{k}_{BC}}=2{k}_{OE},\frac{1}{{k}_{AC}}=2{k}_{OF}$.
∴$\frac{1}{{{k_{AB}}}}+\frac{1}{{{k_{BC}}}}+\frac{1}{{{k_{AC}}}}$=2(kOD+kOE+kOF)=-2=-2.
故選:C.
點評 本題考查了雙曲線的方程、性質,考查了中點弦問題的設而不求思想,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | a≥-2 | B. | a>2 | C. | 0<a<1 | D. | 1≤a<2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|-1<x<2} | D. | {x|-1≤x<2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
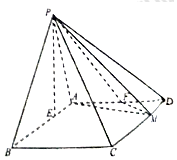 在四棱錐P-ABCD中,底面ABCD為平行四邊形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P點在底面ABCD內的射影E在線段AB上,且PE=2,BE=2EA,F為AD的中點,M在線段CD上,且CM=λCD.
在四棱錐P-ABCD中,底面ABCD為平行四邊形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P點在底面ABCD內的射影E在線段AB上,且PE=2,BE=2EA,F為AD的中點,M在線段CD上,且CM=λCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{7}$ | B. | 7 | C. | $\frac{1}{7}$ | D. | -7 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
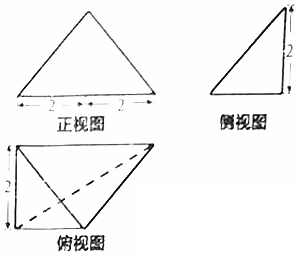
| A. | 4 | B. | $2\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com