
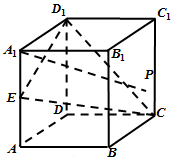
 如圖,棱長為2的正方體ABCD-A1B1C1D1中,E為邊AA1的中點,P為側面BCC1B1上的動點,且A1P∥平面CED1.則點P在側面BCC1B1軌跡的長度為( )
如圖,棱長為2的正方體ABCD-A1B1C1D1中,E為邊AA1的中點,P為側面BCC1B1上的動點,且A1P∥平面CED1.則點P在側面BCC1B1軌跡的長度為( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{2}$ |
分析 取C1D1,C1C的中點G,F,根據線面平行及面面平行的判定定理,可得平面A1GFB∥平面CED1,故A1P∥平面CED1時,P在側面BCC1B1的軌跡是線段BF,進而利用勾股定理,可得答案.
解答 解:取C1D1,C1C的中點G,F,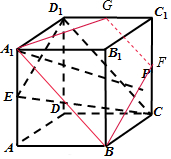
連接A1G、FG,BF,A1B,
∵GF∥D1C,GF?平面CED1,GF∥平面CED1,
BF∥D1E,BF?平面CED1,BF∥平面CED1,
∵BF,GF是平面A1GFB內的相交直線,
∴平面A1GFB∥平面CED1,
故A1P∥平面CED1時,
P在側面BCC1B1的軌跡是線段BF,
∵正方體ABCD-A1B1C1D1的棱長為2,
故BF=$\sqrt{5}$,
故選:C
點評 本題考查的知識點是空間直線與直線,直線與平面的位置關系,難度中檔.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
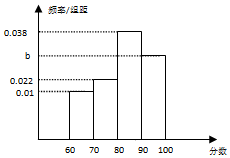 某校舉行“青少年禁毒”知識競賽網上答題,高二年級共有500名學生參加了這次競賽.為了解本次競賽成績情況,從中抽取了100名學生的成績進行統計.請你解答下列問題:
某校舉行“青少年禁毒”知識競賽網上答題,高二年級共有500名學生參加了這次競賽.為了解本次競賽成績情況,從中抽取了100名學生的成績進行統計.請你解答下列問題:| 分組 | 頻數 | 頻率 |
| [60,70) | 10 | 0.1 |
| [70,80) | 22 | 0.22 |
| [80,90) | a | 0.38 |
| [90,100] | 30 | c |
| 合計 | 100 | d |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 有無數條,不一定在平面α內 | B. | 只有一條,不在平面α內 | ||
| C. | 有無數條,一定在平面α內 | D. | 只有一條,且在平面α內 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $(1,\sqrt{2})$ | D. | $\sqrt{2},2)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com