
分析 (1)求出函數的導數,求出m的值,解關于導函數的不等式,求出函數的單調區間,從而求出函數的最小值即可;
(2)問題轉化為(a+1)lnx+$\frac{1}{x}$-ax+a-1>0在x∈(0,1)上恒成立,設h(x)=(a+1)lnx+$\frac{1}{x}$-ax+a-1,x∈(0,+∞),根據函數的單調性求出a的范圍即可.
解答 (1)證明:∵f(x)=(x+m)lnx,
∴f′(x)=lnx+$\frac{x+m}{x}$,
易知圓x2+y2=5在點(2,-1)處的切線方程是2x-y=5,
由題意得f′(e)=2,即lne+$\frac{e+m}{e}$=2,解得:m=0,
∴f(x)=xlnx,f′(x)=lnx+1,
令f′(x)=0,解得:x=$\frac{1}{e}$,
x∈(0,$\frac{1}{e}$)時,f′(x)<0,
故f(x)在(0,$\frac{1}{e}$)遞減,
x∈($\frac{1}{e}$,+∞)時,f′(x)>0,
故f(x)在($\frac{1}{e}$,+∞)遞增,
故f(x)在x=$\frac{1}{e}$處取極小值,也是最小值,最小值是f($\frac{1}{e}$)=-$\frac{1}{e}$,
又-$\frac{1}{e}$>-$\frac{1}{2}$,故f(x)>-$\frac{1}{2}$;
(2)解:若不等式(ax+1)(x-1)<(a+1)lnx在x∈(0,1)上恒成立,
則(a+1)lnx+$\frac{1}{x}$-ax+a-1>0在x∈(0,1)上恒成立,
設h(x)=(a+1)lnx+$\frac{1}{x}$-ax+a-1,x∈(0,+∞),
則h′(x)=$\frac{(1-x)(ax-1)}{{x}^{2}}$,
①a≤0時,h′(x)<0在(0,1)恒成立,
故h(x)在(0,1)遞減,又h(1)=0,
故x∈(0,1)時,總有h(x)>0,符合題意;
②a>1時,令h′(x)=0,解得:x=$\frac{1}{a}$或x=1,
易知h(x)在(0,$\frac{1}{a}$)遞減,在($\frac{1}{a}$,1)遞增,又h(1)=0,
故x∈($\frac{1}{a}$,1)時,總有h(x)<0,不符合題意;
③0<a≤1時,h′(x)<0在(0,1)恒成立,
故h(x)在(0,1)遞減,又h(1)=0,
故x∈(0,1)時,總有h(x)>0,符合題意;
綜上,a的范圍是(-∞,1].
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及轉化思想,考查不等式的證明,是一道綜合題.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:選擇題

| A. | $8+2\sqrt{5}$ | B. | $6+2\sqrt{5}$ | C. | $8+2\sqrt{3}$ | D. | $6+2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
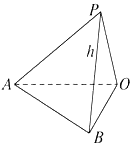 如圖所示,在地面上有一旗桿OP,為測得它的高度h,在地面上取一線段AB,
如圖所示,在地面上有一旗桿OP,為測得它的高度h,在地面上取一線段AB,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
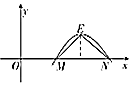 已知奇函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的導函數的部分圖象如圖所示,E是最高點,且△MNE是邊長為1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的導函數的部分圖象如圖所示,E是最高點,且△MNE是邊長為1的正三角形,那么$f({\frac{1}{3}})$=( )| A. | $-\frac{{\sqrt{3}}}{2π}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{3}{4π}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ∅ | B. | {(2,-1)} | C. | {(-1,2),(-2,1)} | D. | {(1,-2),(-1,2),(-2,1)} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com