
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
分析 設(shè)出以M為中點(diǎn)的弦的兩個(gè)端點(diǎn)的坐標(biāo),代入橢圓的方程相減,把中點(diǎn)公式代入,可得弦的斜率與a,b的關(guān)系式,從而求得橢圓的離心率.
解答 解:設(shè)直線x-y+5=0與橢圓相交于A(x1,y1),B(x2,y2),
由x1+x2=-8,y1+y2=2,
直線AB的斜率k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=1,
由$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{{a}^{2}}+\frac{{y}_{1}^{2}}{{b}^{2}}=1}\\{\frac{{x}_{2}^{2}}{{a}^{2}}+\frac{{y}_{2}^{2}}{{b}^{2}}=1}\end{array}\right.$,兩式相減得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{{a}^{2}}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{{b}^{2}}$=0,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$×$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$=1,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{4}$,
由橢圓的離心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,
故選:C.
點(diǎn)評(píng) 本題考查橢圓的標(biāo)準(zhǔn)方程及簡(jiǎn)單性質(zhì),直線與橢圓的位置關(guān)系,考查中點(diǎn)坐標(biāo)公式,“點(diǎn)差法”的應(yīng)用,屬于中檔題.


 優(yōu)翼小幫手同步口算系列答案
優(yōu)翼小幫手同步口算系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知多面體EABCDF的底面是ABCD邊長為2的正方形,EA⊥底面ABCD,F(xiàn)D∥EA,且FD=$\frac{1}{2}$EA=1.
如圖,已知多面體EABCDF的底面是ABCD邊長為2的正方形,EA⊥底面ABCD,F(xiàn)D∥EA,且FD=$\frac{1}{2}$EA=1.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
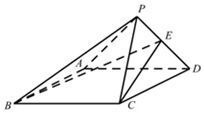 如圖,四棱錐P-ABCD中,底面ABCD邊長為4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;
如圖,四棱錐P-ABCD中,底面ABCD邊長為4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com