Question

20．定義min{a，b}=$\left\{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}\right.$，設函數f（x）=min{$\sqrt{x}$，|x-2|}，若直線y=m與函數y=f（x）的圖象有三個不同的交點，它們的橫坐標分別為x₁，x₂，x₃，則x₁•x₂•x₃的取值范圍為（0，3）．

Answer 1

分析 由f（x）表達式作出函數f（x）的圖象，由圖象可求得符合條件的m的取值范圍，由圖可知0＜x₁＜1＜x₂＜2＜x₃＜3，通過解方程可用m把x₁，x₂，x₃分別表示出來，即可求出得x₁x₂x₃的取值范圍．

解答 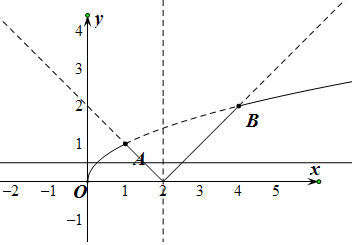解：作出函數f（x）的圖象如下圖所示：
由f（x）=$\left\{\begin{array}{l}{\sqrt{x}}\\{|x-2|}\end{array}\right.$
，解得A（1，1），B（4，2）
由圖象可得，當直線y=m與f（x）圖象有三個交點時m的范圍為：0＜m＜1，
由圖可知0＜x₁＜1＜x₂＜2＜x₃＜3，
則由$\sqrt{{x}_{1}}$=m得x₁=m²，由|x₂-2|=2-x₂=m，
得x₂=2-m，由|x₃-2|=x₃-2=m，
得x₃=m+2，且2-m＞0，m+2＞0，
∴x₁•x₂•x₃=m²•（2-m）•（2+m）=m²•（4-m²）=-（m²-2）²+4，
當m=1時，函數有最大值，即為3，
∴0＜x₁•x₂•x₃≤3．
故答案為：（0，3）

點評 本題考查函數與方程的綜合運用，以及數形結合思想，綜合運用知識分析解決新問題的能力，屬于中檔題．