
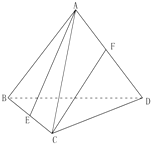
 如圖,在正四面體ABCD(正四面體是所有棱長(zhǎng)都相等的四面體)中,棱長(zhǎng)為2,E、F分別為BC、AD的中點(diǎn).
如圖,在正四面體ABCD(正四面體是所有棱長(zhǎng)都相等的四面體)中,棱長(zhǎng)為2,E、F分別為BC、AD的中點(diǎn).分析 (Ⅰ)求出$\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,$\overrightarrow{CF}=\overrightarrow{CA}+\frac{1}{2}\overrightarrow{AD}$,由此能求出結(jié)果.
(Ⅱ)連接DE,則∠AED為二面角A-BC-D的平面角,由此能求出二面角A-BC-D的余弦值.
解答 解:(Ⅰ)∵在正四面體ABCD(正四面體是所有棱長(zhǎng)都相等的四面體)中,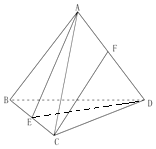
棱長(zhǎng)為2,E、F分別為BC、AD的中點(diǎn),
∴$\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,
$\overrightarrow{CF}=\overrightarrow{CA}+\frac{1}{2}\overrightarrow{AD}$,
∴$\overrightarrow{AE}•\overrightarrow{CF}$=($\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$)•($\overrightarrow{CA}+\frac{1}{2}\overrightarrow{AD}$)
=$\frac{1}{2}\overrightarrow{AB}•\overrightarrow{CA}$+$\frac{1}{2}\overrightarrow{AC}•\overrightarrow{CA}$+$\frac{1}{4}\overrightarrow{AB}•\overrightarrow{AD}$+$\frac{1}{4}\overrightarrow{AC}•\overrightarrow{AD}$
=$\frac{1}{2}×|\overrightarrow{AB}|•|\overrightarrow{CA}|×cos120°$-$\frac{1}{2}×|\overrightarrow{AC}{|}^{2}$+$\frac{1}{4}×|\overrightarrow{AB}|•|\overrightarrow{AD}|×cos60°$+$\frac{1}{4}×|\overrightarrow{AC}|•|\overrightarrow{AD}|×cos60°$
=$\frac{1}{2}×2×2×(-\frac{1}{2})-\frac{1}{2}×{2}^{2}+\frac{1}{4}×2×2×\frac{1}{2}$+$\frac{1}{4}×2×2×\frac{1}{2}$=-2,
∴$\overrightarrow{AE}•\overrightarrow{CF}=-2$.
(Ⅱ)連接DE,則∠AED為二面角A-BC-D的平面角,
∵AB=AC=2,
∴$AE=\sqrt{3},DE=\sqrt{3},AD=2$,
∴$cos∠AED=\frac{1}{3}$,
∴二面角A-BC-D的余弦值為$\frac{1}{3}$.
點(diǎn)評(píng) 本題考查向量的數(shù)量積的求法,考查二面角的余弦值的求法,是中檔題,解題時(shí)要認(rèn)真審題,注意空間思維能力的培養(yǎng).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | f(x)=sinx | B. | f(x)=-|x+1| | ||
| C. | $f(x)=ln\frac{2-x}{2+x}$ | D. | f(x)=$\frac{1}{2}$(ax+a-x),(a>0,a≠1) |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com