
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
分析 利用和與差的正弦公式、誘導公式對已知等式進行變形轉換,得到:sin(α+$\frac{π}{3}$)+cos(α-$\frac{π}{2}$)=$\sqrt{3}$sin(α+$\frac{π}{6}$),然后再利用誘導公式將cos(α+$\frac{2π}{3}$)轉化為-sin(α+$\frac{π}{6}$)的形式,即可解答.
解答 解:∵sin(α+$\frac{π}{3}$)+cos(α-$\frac{π}{2}$)
=sinαcos$\frac{π}{3}$+cosαsin$\frac{π}{3}$+sinα
=$\frac{3}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα
=$\sqrt{3}$($\frac{\sqrt{3}}{2}$sinα+$\frac{1}{2}$cosα)
=$\sqrt{3}$sin(α+$\frac{π}{6}$)
=-$\frac{4\sqrt{3}}{5}$,
∴sin(α+$\frac{π}{6}$)=-$\frac{4}{5}$.
又cos(α+$\frac{2π}{3}$)=cos(α+$\frac{π}{2}$+$\frac{π}{6}$)=-sin(α+$\frac{π}{6}$),
∴cos(α+$\frac{2π}{3}$)=$\frac{4}{5}$.
故選:C.
點評 本題考查了兩角和與差的三角函數,誘導公式的應用,考查計算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
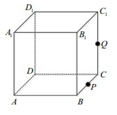 如圖,正方體ABCD-A1B1C1D1的棱長為1,P為BC的中點,Q為線段CC1上的動點,過點A,P,Q的平面截該正方體所得的截面記為S.則下列命題正確的是①②⑤(寫出所有正確命題的編號).
如圖,正方體ABCD-A1B1C1D1的棱長為1,P為BC的中點,Q為線段CC1上的動點,過點A,P,Q的平面截該正方體所得的截面記為S.則下列命題正確的是①②⑤(寫出所有正確命題的編號).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=2x | B. | f(x)=lnx | C. | f(x)=x3 | D. | f(x)=cosx |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{3},\frac{1}{2})$ | C. | $[{\frac{1}{3},1})$ | D. | $[{\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com