
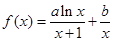 ,曲線
,曲線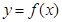 在點
在點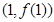 處的切線方程為
處的切線方程為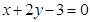 。
。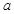 、
、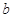 的值;
的值;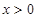 ,且
,且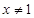 時,
時,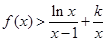 ,求
,求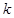 的取值范圍。
的取值范圍。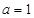 ,
,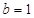 (2)(-
(2)(- ,0]
,0]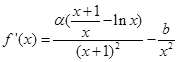
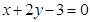 的斜率為
的斜率為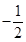 ,且過點
,且過點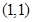 ,故
,故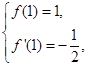 即
即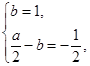
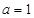 ,
,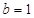 。
。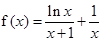 ,所以
,所以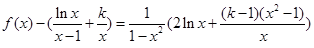 。
。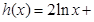

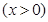 ,則
,則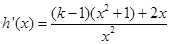 。
。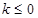 ,由
,由 知,當
知,當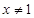 時,
時,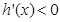 ,h(x)遞減。而
,h(x)遞減。而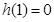 故當
故當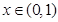 時,
時,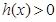 ,可得
,可得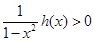 ;
;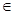 (1,+
(1,+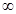 )時,h(x)<0,可得
)時,h(x)<0,可得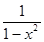 h(x)>0
h(x)>0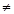 1時,f(x)-(
1時,f(x)-(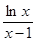 +
+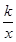 )>0,即f(x)>
)>0,即f(x)>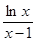 +
+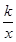 .
.
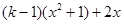 =
=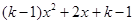 的圖像開口向下,且
的圖像開口向下,且 ,對稱軸x=
,對稱軸x=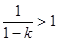 .當x
.當x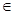 (1,
(1,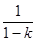 )時,(k-1)(x2 +1)+2x>0,故
)時,(k-1)(x2 +1)+2x>0,故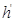 (x)>0,而h(1)=0,故當x
(x)>0,而h(1)=0,故當x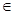 (1,
(1,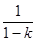 )時,h(x)>0,可得
)時,h(x)>0,可得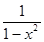 h(x)<0,與題設矛盾。
h(x)<0,與題設矛盾。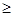 1.此時
1.此時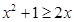 ,
,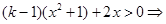
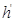 (x)>0,而h(1)=0,故當x
(x)>0,而h(1)=0,故當x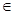 (1,+
(1,+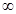 )時,h(x)>0,可得
)時,h(x)>0,可得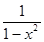 h(x)<0,與題設矛盾。
h(x)<0,與題設矛盾。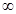 ,0]
,0]

科目:高中數學 來源:不詳 題型:解答題
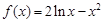
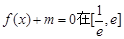 內有兩個不等的實根,求實數m的取值范圍;(e為自然對數的底數)
內有兩個不等的實根,求實數m的取值范圍;(e為自然對數的底數)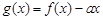 的圖象與x軸交于兩點
的圖象與x軸交于兩點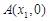 、
、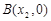 且
且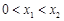 .求證:
.求證: (其中正常數
(其中正常數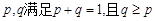 ).
).查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 ,
, ,
, ,其中
,其中 。
。 與
與 的圖像在交點(2,
的圖像在交點(2, )處的切線互相垂直,
)處的切線互相垂直, 的值;
的值; 是函數
是函數 的一個極值點,
的一個極值點, 和1是
和1是 的兩個零點,
的兩個零點, ∈(
∈(
 ,求
,求 ;
; 時,若
時,若 ,
, 是
是 的兩個極值點,當|
的兩個極值點,當| -
- |>1時,
|>1時, -
- |
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com