【題目】某大學為了調查該校學生性別與身高的關系，對該校1000名學生按照
的比例進行抽樣調查，得到身高頻數分布表如下：
男生身高頻率分布表
男生身高 （單位：厘米） |
|
|
|
|
|
|
頻數 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高頻數分布表
女生身高 （單位：厘米） |
|
|
|
|
|
|
頻數 | 3 | 10 | 15 | 6 | 3 | 3 |
（1）估計這1000名學生中女生的人數；
（2）估計這1000名學生中身高在
的概率；
（3）在樣本中，從身高在
的女生中任取2名女生進行調查，求這2名學生身高在
的概率.（身高單位：厘米）
【答案】（1）400名；（2）0.49；（3）
.
【解析】
（1）由男生、女生身高頻數分布表可知，抽了60名男生，40名女生，則女生的人數為
；
（2）由男生、女生身高頻數分布表可知，身高在
的有49人，又共抽取100人，計算可得概率；
（3）身高在
的女生有3名，身高在
的女生有3名，列舉法可得抽取2名共15種，其中2名學生的身高都在的情況有3種，可求概率.
（1）由頻率分布表可得樣本中男生為60名，女生為40名，
估計這1000名學生中女生的人數大約是（名）.
（2）由表知，樣本中身高在的人數為
，
樣本容量是100，
樣本中身高在的概率為
，
估計這1000名學生中身高在的概率為0.49.
（3）依題意，身高在的女生有3名，記為
，
，
，
身高在的女生有3名，記為
，
，
，
則從身高在
的女生中任取2名，
所有情況有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共15種，
其中2名學生的身高都在的情況有，，共3種，
這2名學生身高都在的概率為
.
科目：高中數學 來源： 題型：
【題目】某鄉鎮為了打贏脫貧攻堅戰，決定盤活貧困村的各項經濟發展要素，實施了產業、創業、就業“三業并舉”工程.在實施過程中，引導某貧困村農戶因地制宜開展種植某經濟作物.該類經濟作物的質量以其質量指標值來衡量，質量指標值越大表明質量越好，記其質量指標值為
，其質量指標的等級劃分如下表1：
表1
質量指標值 | 產品等級 |
| 優秀品 |
| 良好品 |
| 合格品 |
| 不合格品 |
為了解該類經濟作物在當地的種植效益，當地引種了甲、乙兩個品種.并隨機抽取了甲、乙兩個品種的各
件產品，測量了每件產品的質量指標值，得到下面產品質量指標值頻率分布直方圖（圖1和圖2）.
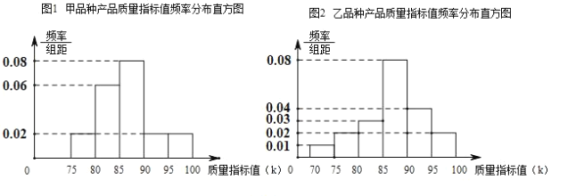
（1）若將頻率視為概率，從乙品種產品中有放回地隨機抽取
件，記“抽出乙品種產品中至少
件良好品或以上”為事件
，求事件發生的概率
；(結果保留小數點后位)(參考數值：
，
)
（2）若甲、乙兩個品種的銷售利潤率
與質量指標值滿足表2
表2
質量指標值 |
|
|
|
|
銷售利潤率 |
|
|
|
|
其中
，試分析，從長期來看，種植甲、乙哪個品種的平均利潤率較大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
三個班共有
名學生，為調查他們的上網情況，通過分層抽樣獲得了部分學生一周的上網時長，數據如下表（單位：小時）：
|
|
|
|
|
|
（1）試估計
班的學生人數；
（2）從這120名學生中任選1名學生，估計這名學生一周上網時長超過15小時的概率；
（3）從A班抽出的6名學生中隨機選取2人，從B班抽出的7名學生中隨機選取1人，求這3人中恰有2人一周上網時長超過15小時的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
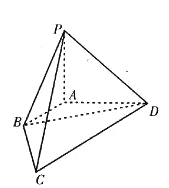
【題目】如圖，在四棱錐
中，已知棱
，
，
兩兩垂直，長度分別為1，2，2.若
（
），且向量
與
夾角的余弦值為
.
（1）求
的值；
（2）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設等差數列
的公差
，數列
的前
項和為
，滿足
，且
，
.若實數
，則稱
具有性質
.
（1）請判斷
、
是否具有性質
，并說明理由；
（2）設
為數列的前項和，
，且
恒成立.求證：對任意的
，實數
都不具有性質；
（3）設
是數列
的前項和，若對任意的
，
都具有性質，求所有滿足條件的的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】請你設計一個包裝盒，如圖所示，ABCD是邊長為60cm的正方形硬紙片，切去陰影部分所示的四個全等的等腰直角三角形，再沿虛線折起，使得
四個點重合于圖中的點P，正好形成一個正四棱柱形狀的包裝盒，E、F在AB上是被切去的等腰直角三角形斜邊的兩個端點，設AE=FB=xcm2
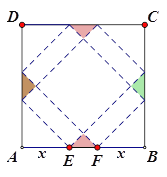
（1）若廣告商要求包裝盒側面積S（cm
）最大，試問x應取何值？
（2）若廣告商要求包裝盒容積V（cm
）最大，試問x應取何值？并求出此時包裝盒的高與底面邊長的比值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，
，上頂點為A，過的直線
與y軸交于點M，滿足
（O為坐標原點），且直線l與直線
之間的距離為
.
（1）求橢圓C的方程；
（2）在直線
上是否存在點P，滿足
？存在，指出有幾個這樣的點（不必求出點的坐標）；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知O為坐標原點，拋物線C：y2=8x上一點A到焦點F的距離為6，若點P為拋物線C準線上的動點，則|OP|+|AP|的最小值為（ ）
A. 4B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
