
定義:若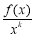 在
在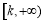 上為增函數,則稱
上為增函數,則稱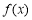 為“k次比增函數”,其中
為“k次比增函數”,其中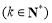 . 已知
. 已知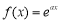 其中e為自然對數的底數.
其中e為自然對數的底數.
(1)若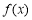 是“1次比增函數”,求實數a的取值范圍;
是“1次比增函數”,求實數a的取值范圍;
(2)當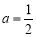 時,求函數
時,求函數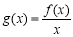 在
在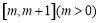 上的最小值;
上的最小值;
(3)求證: .
.
(1) 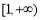 ;(2)詳見解析;(3)詳見解析.3.詳見解析.
;(2)詳見解析;(3)詳見解析.3.詳見解析.
【解析】
試題分析:(Ⅰ)由于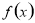 是“1次比增函數”,得到
是“1次比增函數”,得到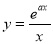 在
在 上為增函數,求導后,導數大于等于0,分離參數
上為增函數,求導后,導數大于等于0,分離參數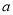 ,轉化為恒成立,求最值的問題,即可得到實數a的取值范圍;
,轉化為恒成立,求最值的問題,即可得到實數a的取值范圍;
(Ⅱ)當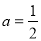 時,得到函數
時,得到函數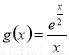 ,
, ,利用導數即可得到
,利用導數即可得到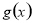 的單調區間,分成
的單調區間,分成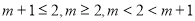 ,三種情況進行分類討論即可函數在
,三種情況進行分類討論即可函數在
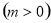 上單調性,進而得到其最小值;
上單調性,進而得到其最小值;
(Ⅲ)由(Ⅱ)當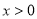 時,
時, ,即
,即 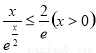 ,則
,則 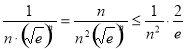 ,即可證明:
,即可證明: .,
.,
試題解析:(1)由題意知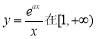 上為增函數,因為
上為增函數,因為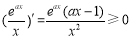 在
在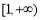 上
上
恒成立.又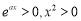 ,則
,則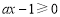 在
在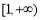 上恒成立,
上恒成立,
即 在
在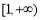 上恒成立. 而當
上恒成立. 而當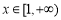 時,
時,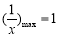 ,所以
,所以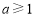 ,
,
于是實數a的取值范圍是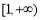 . 4分
. 4分
(2)當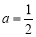 時,
時,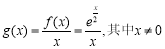 ,則
,則 .
.
當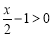 ,即
,即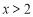 時,
時,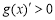 ;
;
當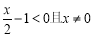 ,即
,即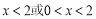 時,
時,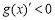 .
.
則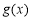 的增區間為(2,+∞),減區間為(-∞,0),(0,2). 6分
的增區間為(2,+∞),減區間為(-∞,0),(0,2). 6分
因為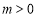 ,所以
,所以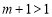 ,
,
①當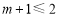 ,即
,即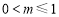 時,
時,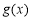 在[
在[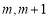 ]上單調遞減,
]上單調遞減,
所以 .
.
②當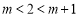 ,即
,即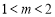 時,
時,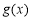 在
在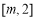 上單調遞減,
上單調遞減,
在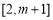 上單調遞增,所以
上單調遞增,所以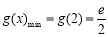 .
.
③當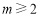 時,
時,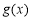 在[
在[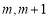 ]上單調遞增,所以
]上單調遞增,所以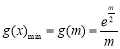 .
.
綜上,當 時,
時, ;
;
當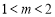 時,
時,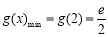 ;
;
當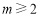 時,
時,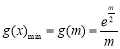 . 9分
. 9分
(3)由(2)可知,當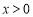 時,
時,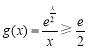 ,所以
,所以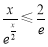
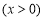 ,
,
可得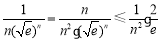 11分
11分
于是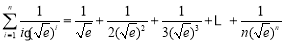
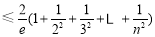
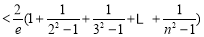

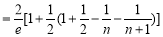
 14分
14分
考點:1.利用導數研究函數的單調性;2.利用導數求函數的最值.


科目:高中數學 來源:2013-2014學年湖北省黃岡市高三下學期三月月考文科數學試卷(解析版) 題型:填空題
設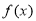 是定義在
是定義在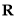 上的增函數,且對于任意的
上的增函數,且對于任意的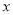 都有
都有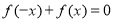 恒成立. 如果實數
恒成立. 如果實數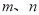 滿足不等式
滿足不等式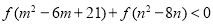 ,xxk那么
,xxk那么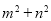 的取值范圍是
的取值范圍是
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省武漢市高三下學期4月調研測試文科數學試卷(解析版) 題型:選擇題
在△ABC中,角A,B,C的對邊分別為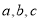 ,若A,B,C成等差數列,
,若A,B,C成等差數列,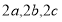 成等比數列,則
成等比數列,則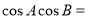 ( )
( )
A.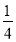 B.
B.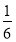 C.
C.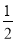 D.
D.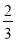
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省宜昌示范教學協作體高一下學期期中考試數學試卷(解析版) 題型:選擇題
已知點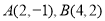 ,點
,點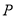 在
在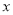 軸上,當
軸上,當 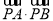 取最小值時,
取最小值時,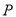 點的坐標是( )
點的坐標是( )
A.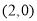 B.
B.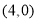 C.
C.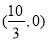 D.
D.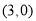
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省天門市畢業生四月調研考試理科數學試卷(解析版) 題型:解答題
設函數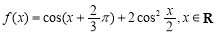 .
.
(1)求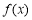 的值域;
的值域;
(2)記△ABC的內角A,B,C的對邊長分別為a,b,c,若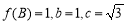 ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省天門市畢業生四月調研考試理科數學試卷(解析版) 題型:選擇題
某企業擬建造如圖所示的容器(不計厚度,長度單位:米),其中容器的中間為圓柱形,左右兩端均為半球形,按照設計要求容器的容積為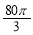 立方米,且
立方米,且 . 假設該容器的建造費用僅與其表面積有關. 已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為22千元. 設該容器的建造費用為y千元. 當該容器建造費用最小時,r的值為( )
. 假設該容器的建造費用僅與其表面積有關. 已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為22千元. 設該容器的建造費用為y千元. 當該容器建造費用最小時,r的值為( )
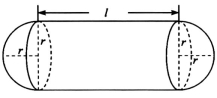
A.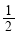 B.1 C.
B.1 C.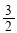 D.2
D.2
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省天門市畢業生四月調研考試文科數學試卷(解析版) 題型:填空題
分別在區間[1,6]和[1,4]內任取一個實數,依次記為m和n,則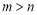 的概率為
的概率為
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省七市(州)高三年級聯合考試文科數學試卷(解析版) 題型:解答題
已知向量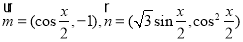 ,設函數
,設函數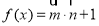 .
.
(1)求函數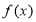 的單調遞增區間;
的單調遞增區間;
(2)在 中,角
中,角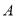 、
、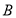 、
、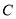 的對邊分別為
的對邊分別為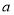 、
、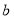 、
、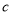 ,且滿足
,且滿足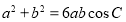 ,
,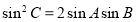 ,求
,求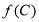 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com