
分析 (1)由函數f(x)=ax+b(a>0且a≠1)的圖象經過點(2,0),(0,-2),可得$\left\{\begin{array}{l}{a}^{2}+b=0\\ 1+b=-2\end{array}\right.$,解得a和b的值;
(2)由(1)得f(x)=$\sqrt{3}$x-3,當x∈[2,4]時,函數y=f(x)為增函數,進而可得函數的最值.
解答 解:(1)∵函數f(x)=ax+b(a>0且a≠1)的圖象經過點(2,0),(0,-2).
∴$\left\{\begin{array}{l}{a}^{2}+b=0\\ 1+b=-2\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=\sqrt{3}\\ b=-3\end{array}\right.$,
(2)由(1)得f(x)=$\sqrt{3}$x-3,
當x∈[2,4]時,函數y=f(x)為增函數,
故當x=2時,函數y=f(x)的最小值為0,
當x=4時,函數y=f(x)的最大值為6.
點評 本題考查的知識點是函數的最值及其幾何意義,函數解析式的求法,難度基礎.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | N>M>K | B. | K>M>N | C. | M>K>N | D. | M>N>K |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $?{x_0}∈R,{2^{{x_0}-1}}≥1$ | B. | $?{x_0}∈R,{2^{{x_0}-1}}>1$ | ||
| C. | ?x∈R,2x-1≤1 | D. | ?x∈R,2x-1>1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
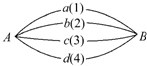 如圖,從A地到B地設置了4條不同的網絡線路,它們通過的最大信息量分別為1,2,3,4,現從中任取三條網線連通A,B兩地(三條網線可通過的信息總量即三條網線各自的最大信息量之和).
如圖,從A地到B地設置了4條不同的網絡線路,它們通過的最大信息量分別為1,2,3,4,現從中任取三條網線連通A,B兩地(三條網線可通過的信息總量即三條網線各自的最大信息量之和).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
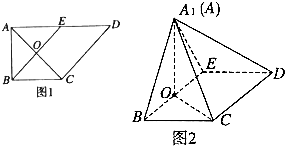 如圖1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中點,O是AC與BE的交點.將△ABE沿BE折起到△A1BE的位置,如圖2.
如圖1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中點,O是AC與BE的交點.將△ABE沿BE折起到△A1BE的位置,如圖2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com