
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 首先化簡三角函數式,根據f(-$\frac{π}{6}$)=$\frac{3}{4}$,得到ω的兩個等式,由題意取ω的最小正數.
解答 解:f(x)=sin(ωx+$\frac{π}{3}$)-$\frac{1}{2}$cos(ωx-$\frac{7π}{6}$)
=sin(ωx)cos$\frac{π}{3}$+cos(ωx)sin$\frac{π}{3}$)-$\frac{1}{2}$cos(ωx)cos$\frac{7π}{6}$-$\frac{1}{2}$sin(ωx)sin$\frac{7π}{6}$
=$\frac{3}{4}$sin(ωx)+$\frac{3\sqrt{3}}{4}$cos(ωx)
=$\frac{3}{2}$sin(ωx+$\frac{π}{3}$),
又f(-$\frac{π}{6}$)=$\frac{3}{4}$,所以sin($-\frac{π}{6}$ω+$\frac{π}{3}$)=$\frac{1}{2}$,所以ω=1-12k或ω=-3-12k,k∈Z,所以滿足題意的ω的最小值為1.
故選C.
點評 本題考查了三角函數式的化簡與求值;熟練正確的對解析式化簡是解答的前提.


科目:高中數學 來源: 題型:解答題
 如圖 已知四邊形 ABCD 為直角梯形,AB⊥AD,DC∥AB,且邊 AB、AD、DC 的長分別為 7cm,4cm,4cm,分別以 AB、AD、DC 三邊所在直線為旋轉軸,求所得幾何體體積.
如圖 已知四邊形 ABCD 為直角梯形,AB⊥AD,DC∥AB,且邊 AB、AD、DC 的長分別為 7cm,4cm,4cm,分別以 AB、AD、DC 三邊所在直線為旋轉軸,求所得幾何體體積.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | b<c<a |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-$\frac{2}{3}$,0] | B. | (-∞,0)∪[$\frac{2}{3}$,+∞) | C. | [0,$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$]∪[0,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
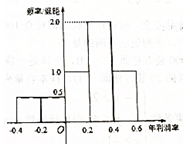 某公司計劃明年用不超過6千萬元的資金投資于本地養魚場和遠洋捕撈隊.經過本地養魚場年利潤率的調研,得到如圖所示年利潤率的頻率分布直方圖.對遠洋捕撈隊的調研結果是:年利潤率為60%的可能性為0.6,不賠不賺的可能性為0.2,虧損30%的可能性為0.2.假設該公司投資本地養魚場的資金為x(x≥0)千萬元,投資遠洋捕撈隊的資金為y(y≥0)千萬元.
某公司計劃明年用不超過6千萬元的資金投資于本地養魚場和遠洋捕撈隊.經過本地養魚場年利潤率的調研,得到如圖所示年利潤率的頻率分布直方圖.對遠洋捕撈隊的調研結果是:年利潤率為60%的可能性為0.6,不賠不賺的可能性為0.2,虧損30%的可能性為0.2.假設該公司投資本地養魚場的資金為x(x≥0)千萬元,投資遠洋捕撈隊的資金為y(y≥0)千萬元.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 為了解甲、乙兩廠產品的質量,從甲廠生產的產品中隨機抽取3件樣品,從乙廠生產的產品中隨機抽取4件樣品,測量產品中某種元素的含量(單位:毫克),如圖是測量數據的莖葉圖.若它們的中位數相同,平均數也相同,則圖中的m,n的比值$\frac{m}{n}$=( )
為了解甲、乙兩廠產品的質量,從甲廠生產的產品中隨機抽取3件樣品,從乙廠生產的產品中隨機抽取4件樣品,測量產品中某種元素的含量(單位:毫克),如圖是測量數據的莖葉圖.若它們的中位數相同,平均數也相同,則圖中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 人數 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com