
分析 (1)由題意可知,右焦點在圓上或在圓的外部,因此c≥b.即c2≥b2=a2-c2,解出即可得出.
(2)依題意,設直線l:$y=\frac{{\sqrt{3}}}{3}({x-c})$,由l與圓x2+y2=b2相切得$\frac{{|{\frac{{\sqrt{3}}}{3}c}|}}{{\sqrt{1+{{({\frac{{\sqrt{3}}}{3}})}^2}}}}=b$,化簡即可得出.
(3)設原點關于直線l對稱的點為M(x,y),則M到原點的距離為2b,M到焦點F(c,0)的距離為c.由$\left\{{\begin{array}{l}{{x^2}+{y^2}={{({2b})}^2}}\\{{{({x-c})}^2}+{y^2}={c^2}}\end{array}}\right.$,解出代入橢圓方程解出離心率,比較即可判斷出結論.
解答 解:(1)由題意可知,右焦點在圓上或在圓的外部,因此c≥b.
∴c2≥b2=a2-c2,也即$\frac{c^2}{a^2}≥\frac{1}{2}$,解之可得$\frac{{\sqrt{2}}}{2}≤e<1$.
∴橢圓的離心率e的取值范圍是$[{\frac{{\sqrt{2}}}{2},1})$.
(2)依題意,設直線l:$y=\frac{{\sqrt{3}}}{3}({x-c})$,由l與圓x2+y2=b2相切得$\frac{{|{\frac{{\sqrt{3}}}{3}c}|}}{{\sqrt{1+{{({\frac{{\sqrt{3}}}{3}})}^2}}}}=b$,即c2=4b2,
∴c2=4(a2-c2),解得$e=\frac{{2\sqrt{5}}}{5}$.
(3)設原點關于直線l對稱的點為M(x,y),則M到原點的距離為2b,M到焦點F(c,0)的距離為c.
由$\left\{{\begin{array}{l}{{x^2}+{y^2}={{({2b})}^2}}\\{{{({x-c})}^2}+{y^2}={c^2}}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{x={{\frac{2b}{c}}^2}}\\{{y^2}=\frac{{4{b^2}{c^2}-4{b^4}}}{c^2}}\end{array}}\right.$,代入橢圓方程可得4b2=3a2,易得$e=\frac{1}{2}$
這與$\frac{{\sqrt{2}}}{2}≤e<1$矛盾,故離心率不存在.
點評 本題考查了橢圓底邊在方程及其性質、直線與圓相切的性質、點到直線的距離公式,考查了推理能力與計算能力,屬于難題.


科目:高中數學 來源: 題型:選擇題
| A. | 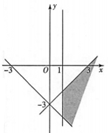 | B. | 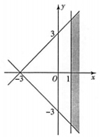 | C. | 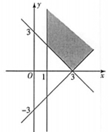 | D. | 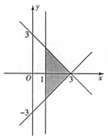 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}i$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
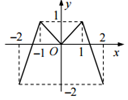 如圖,定義在[-2,2]的偶函數f(x)的圖象如圖所示,函數g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零點個數為( )
如圖,定義在[-2,2]的偶函數f(x)的圖象如圖所示,函數g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零點個數為( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,5) | B. | (5,10) | C. | (10,15) | D. | (15,20) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
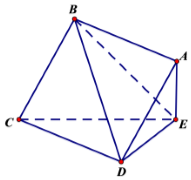 如圖,邊長為2的正方形ABCD所在平面與三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.
如圖,邊長為2的正方形ABCD所在平面與三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com