Question

11．已知函數f（x）=$\left\{\begin{array}{l}{x+2，x≤-1}\\{{x}^{2，}-1＜x＜2}\\{2x，x≥2}\end{array}\right.$．
（1）求f（f（-2））；
（2）畫出函數f（x）的圖象，根據圖象寫出函數的單調增區間并求出函數f（x）在區間（-4，0）上的值域．

Answer 1

分析 （1）利用分段函數求解函數值即可．
（2）畫出函數的圖象，利用函數的圖象寫出函數的單調增區間并求出函數f（x）在區間（-4，0）上的值域．

解答 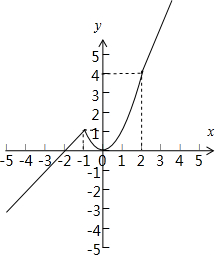解：（1）函數f（x）=$\left\{\begin{array}{l}{x+2，x≤-1}\\{{x}^{2，}-1＜x＜2}\\{2x，x≥2}\end{array}\right.$．
f（-2）=-2+2=0，
f（f（-2））=f（0）=0.3分
（2）函數的圖象如圖：…（6分）
單調增區間為（-∞，-1），（0，+∞）（開區間，閉區間都給分）…（9分）
由圖可知：
f（-4）=-2，f（-1）=1，
函數f（x）在區間（-4，0）上的值域（-2，1]．…12分．

點評 本題考查分段函數的應用，函數的圖象的畫法，二次函數的簡單性質的應用，考查數形結合以及計算能力．