
【題目】已知函數(shù)![]() .
.
(1)設(shè)![]() 是
是![]() 的極值點,求
的極值點,求![]() ,并求
,并求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當![]() 時,證明
時,證明![]() .
.
【答案】(1)![]() ,
,![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,增區(qū)間為
,增區(qū)間為![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)求出導函數(shù),由![]() 求得
求得![]() ,再確定
,再確定![]() 的正負,從而確定
的正負,從而確定![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)由![]() 得
得![]() ,
,![]() ,構(gòu)造新函數(shù)
,構(gòu)造新函數(shù)![]() ,
,![]() ,只要證明
,只要證明![]() 即可,利用導數(shù)求出
即可,利用導數(shù)求出![]() 的最小值即可.只是要注意
的最小值即可.只是要注意![]() 的唯一解
的唯一解![]() 不可直接得出,只能通過
不可直接得出,只能通過![]() 的零點
的零點![]() 來研究
來研究![]() 的最小值
的最小值![]() ,只要說明
,只要說明![]() 即可.
即可.
(1)![]() ,
,
由![]() 是
是![]() 的極值點知,
的極值點知,![]() ,即
,即![]() ,所以
,所以![]() .
.
于是![]() ,定義域為
,定義域為![]() ,且
,且![]() ,
,
函數(shù)![]() 在
在![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]() ,
,
因此當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,增區(qū)間為
,增區(qū)間為![]() .
.
(2)當![]() ,
,![]() 時,
時,![]() ,從而
,從而![]() ,則
,則
![]() ,
,
令![]() ,
,![]() ,則
,則
![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
且![]() ,
,![]() ,
,
故存在唯一的實數(shù)![]() ,使得
,使得![]() .
.
當![]() 時,
時,![]() ,
,![]() 遞減;當
遞減;當![]() 時,
時,![]() ,
,![]() 遞增.
遞增.
從而當![]() 時,
時,![]() 取最小值.
取最小值.
由![]() 得
得![]() ,則
,則![]() ,
,![]() ,
,
故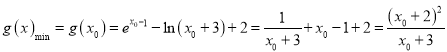 ,
,
由![]() 知,
知,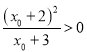 ,故
,故![]() ,
,
即當![]() 時,
時,![]() 成立.
成立.


科目:高中數(shù)學 來源: 題型:
【題目】已知長方體![]() ,
,![]() ,
,![]() ,
,![]() ,已知P是矩形
,已知P是矩形![]() 內(nèi)一動點,
內(nèi)一動點,![]() 與平面
與平面![]() 所成角為
所成角為![]() ,設(shè)P點形成的軌跡長度為
,設(shè)P點形成的軌跡長度為![]() ,則
,則![]() _________;當
_________;當![]() 的長度最短時,三棱錐
的長度最短時,三棱錐![]() 的外接球的表面積為_____________.
的外接球的表面積為_____________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線C的頂點為坐標原點O,對稱軸為![]() 軸,其準線為
軸,其準線為![]() .
.
(1)求拋物線C的方程;
(2)設(shè)直線![]() ,對任意的
,對任意的![]() 拋物線C上都存在四個點到直線l的距離為
拋物線C上都存在四個點到直線l的距離為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,正方形![]() 邊長為
邊長為![]() ,將
,將![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,使得二面角
的位置,使得二面角![]() 的大小為
的大小為![]() .
.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)點![]() 在直線
在直線![]() 上,且直線
上,且直線![]() 與平面
與平面![]() 所成角正弦值為
所成角正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在疫情這一特殊時期,教育行政部門部署了“停課不停學”的行動,全力幫助學生在線學習.復課后進行了摸底考試,某校數(shù)學教師為了調(diào)查高三學生這次摸底考試的數(shù)學成績與在線學習數(shù)學時長之間的相關(guān)關(guān)系,對在校高三學生隨機抽取45名進行調(diào)查.知道其中有25人每天在線學習數(shù)學的時長是不超過1小時的,得到了如下的等高條形圖:
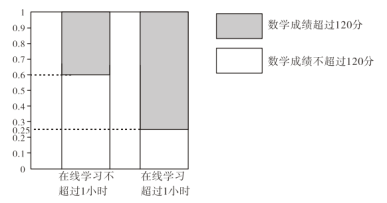
(Ⅰ)將頻率視為概率,求學習時長不超過1小時但考試成績超過120分的概率;
(Ⅱ)是否有![]() 的把握認為“高三學生的這次摸底考試數(shù)學成績與其在線學習時長有關(guān)”.
的把握認為“高三學生的這次摸底考試數(shù)學成績與其在線學習時長有關(guān)”.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
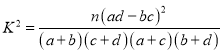
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】第41屆世界博覽會于2010年5月1日至10月31日,在中國上海舉行,氣勢磅礴的中國館——“東方之冠”令人印象深刻,該館以“東方之冠,鼎盛中華,天下糧倉,富庶百姓”為設(shè)計理念,代表中國文化的精神與氣質(zhì).其形如冠蓋,層疊出挑,制似斗拱.它有四根高33.3米的方柱,托起斗狀的主體建筑,總高度為60.3米,上方的“斗冠”類似一個倒置的正四棱臺,上底面邊長是139.4米,下底面邊長是69.9米,則“斗冠”的側(cè)面與上底面的夾角約為( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知傾斜角為![]() 的直線經(jīng)過拋物線
的直線經(jīng)過拋物線![]() 的焦點
的焦點![]() ,與拋物線
,與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)設(shè)![]() 為拋物線
為拋物線![]() 上任意一點(異于頂點),過
上任意一點(異于頂點),過![]() 做傾斜角互補的兩條直線
做傾斜角互補的兩條直線![]() 、
、![]() ,交拋物線
,交拋物線![]() 于另兩點
于另兩點![]() 、
、![]() ,記拋物線
,記拋物線![]() 在點
在點![]() 的切線
的切線![]() 的傾斜角為
的傾斜角為![]() ,直線
,直線![]() 的傾斜角為
的傾斜角為![]() ,求證:
,求證:![]() 與
與![]() 互補.
互補.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com