
分析 求出x<0時,函數f(x)的解析式,畫出R上的圖象,構造f(x)與y=$\frac{1}{π}$交點問題,利用對稱性求解,注意確定交點坐標求解.
解答 解:∵定義在R上的奇函數f(x),當x≥0時,$f(x)=\left\{\begin{array}{l}\frac{-2x}{x+1},x∈[0,1)\\ 1-|x-3|,x∈[1,+∞)\end{array}\right.$,
∴x<0時,f(x)=$\left\{\begin{array}{l}{\frac{-2x}{1-x},x∈(-1,0]}\\{|x+3|-1,x∈(-∞,-1]}\end{array}\right.$畫出圖象:
∵函數F(x)=f(x)-$\frac{1}{π}$,
∴f(x)與y=$\frac{1}{π}$交點的橫坐標,
根據圖象可設交點的橫坐標從左到右為x1,x2,x3,x4,x5,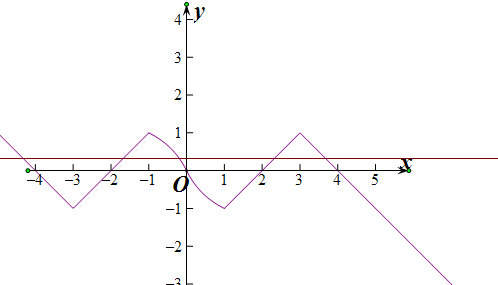
根據圖象的對性可知;x1+x2=-6,x4+x5=6,
∴x1+x2=x3=x4=x5=x3,
∵$\frac{-2x}{1-x}$=$\frac{1}{π}$,x=$\frac{1}{1-2π}$,
故函數F(x)=f(x)-$\frac{1}{π}$的所有零點之和為:$\frac{1}{1-2π}$.
故答案為:$\frac{1}{1-2π}$.
點評 本題考查了函數的奇偶性,圖象的對稱性,函數的零點與構造函數交點的問題,屬于中檔題,關鍵是確定函數解析式,畫圖象.考查數形結合轉化思想應用.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:解答題
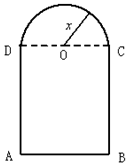 如圖,用長為12m的鐵絲彎成下部為矩形,上部為半圓形的框架窗戶,若半圓半徑
如圖,用長為12m的鐵絲彎成下部為矩形,上部為半圓形的框架窗戶,若半圓半徑查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
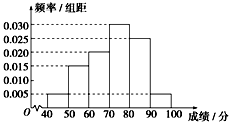 某校從參加高二年級學業水平測試的學生中抽出80名學生,其數學成績 (均為整數)的頻率分布直方圖如圖所示.估計這次測試中數學成績的平均分為72,眾數為75.
某校從參加高二年級學業水平測試的學生中抽出80名學生,其數學成績 (均為整數)的頻率分布直方圖如圖所示.估計這次測試中數學成績的平均分為72,眾數為75.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com