
【題目】設![]() 是橢圓
是橢圓![]() 上的兩點,已知向量
上的兩點,已知向量![]() ,
,![]() ,若
,若![]() 且橢圓的離心率
且橢圓的離心率![]() ,短軸長為2,
,短軸長為2,![]() 為坐標原點.
為坐標原點.
(1)求橢圓的方程;
(2)若直線![]() 過橢圓的焦點
過橢圓的焦點![]() (
(![]() 為半焦距),求直線
為半焦距),求直線![]() 的斜率
的斜率![]() 的值;
的值;
(3)試問:![]() 的面積是否為定值?如果是,請給予證明;如果不是,請說明理由.
的面積是否為定值?如果是,請給予證明;如果不是,請說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)三角形的面積為定值1.
;(Ⅲ)三角形的面積為定值1.
【解析】
試題(1)根據條件可得![]() ,再設直線
,再設直線![]() 的方程為:
的方程為:![]() ,與橢圓聯立方程組,利用韋達定理和已知條件
,與橢圓聯立方程組,利用韋達定理和已知條件![]() ,即可求出
,即可求出![]() 的值;(2)先考慮直線
的值;(2)先考慮直線![]() 斜率不存在的情況,即
斜率不存在的情況,即![]() ,
,![]() ,根據
,根據![]() ,求得
,求得![]() 和
和![]() 的關系式,代入橢圓的方程求得
的關系式,代入橢圓的方程求得![]() 點的橫坐標和縱坐標的絕對值,進而求得△AOB的面積的值;當直線
點的橫坐標和縱坐標的絕對值,進而求得△AOB的面積的值;當直線![]() 斜率存在時,設出直線
斜率存在時,設出直線![]() 的方程,與橢圓聯立方程組,利用韋達定理表示出
的方程,與橢圓聯立方程組,利用韋達定理表示出![]() 和
和![]() ,再利用
,再利用![]() ,弦長公式及三角形面積公式求得答案.
,弦長公式及三角形面積公式求得答案.
試題解析:(1)由題可得:![]() ,
,![]() ,所以,橢圓的方程為
,所以,橢圓的方程為![]()
設![]() 的方程為:
的方程為:![]() ,代入
,代入![]() 得:
得:![]()
∴![]() ,
,![]() ,
,![]()
∵![]() ,∴
,∴![]() ,即:
,即: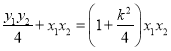
![]()
即![]() ,解得:
,解得:![]()
(2)①直線![]() 斜率不存在時,即
斜率不存在時,即![]() ,
,![]()
∵![]()
∴![]() ,即
,即![]()
又∵![]() 點在橢圓上
點在橢圓上
∴![]() ,即
,即![]()
∴![]() ,
,![]()
∴![]() ,故
,故![]() 的面積為定值1
的面積為定值1
②當直線![]() 斜率存在時,設
斜率存在時,設![]() 的方程為
的方程為![]() ,
,
聯立 得:
得:![]()
∴![]() ,
,![]() ,
,![]()
∴![]()
![]()
![]()
所以三角形的面積為定值1.


科目:高中數學 來源: 題型:
【題目】運動健康已成為大家越來越關心的話題,某公司開發的一個類似計步數據庫的公眾號.手機用戶可以通過關注該公眾號查看自己每天行走的步數,同時也可以和好友進行運動量的PK和點贊.現從張華的好友中隨機選取40人(男、女各20人),記錄他們某一天行走的步數,并將數據整理如表:
步數 性別 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
(1)若某人一天行走的步數超過8000步被評定為“積極型”,否則被評定為“懈怠型”,根據題意完成下列2×2列聯表,并據此判斷能否有90%的把握認為男、女的“評定類型”有差異?
積極型 | 懈怠型 | 總計 | |
男 | |||
女 | |||
總計 |
(2)在張華的這40位好友中,從該天行走的步數不超過5000步的人中隨機抽取2人,設抽取的女性有X人,求X=1時的概率.
參考公式與數據:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.在購進機器時,可以一次性額外購買幾次維修服務,每次維修服務費用200元,另外實際維修一次還需向維修人員支付小費,小費每次50元.在機器使用期間,如果維修次數超過購機時購買的維修服務次數,則每維修一次需支付維修服務費用500元,無需支付小費.現需決策在購買機器時應同時一次性購買幾次維修服務,為此搜集并整理了100臺這種機器在三年使用期內的維修次數,得下面統計表:
維修次數 | 8 | 9 | 10 | 11 | 12 |
頻數 | 10 | 20 | 30 | 30 | 10 |
記x表示1臺機器在三年使用期內的維修次數,y表示1臺機器在維修上所需的費用(單位:元),![]() 表示購機的同時購買的維修服務次數.
表示購機的同時購買的維修服務次數.
(1)若![]() =10,求y與x的函數解析式;
=10,求y與x的函數解析式;
(2)若要求“維修次數不大于![]() ”的頻率不小于0.8,求n的最小值;
”的頻率不小于0.8,求n的最小值;
(3)假設這100臺機器在購機的同時每臺都購買10次維修服務,或每臺都購買11次維修服務,分別計算這100臺機器在維修上所需費用的平均數,以此作為決策依據,購買1臺機器的同時應購買10次還是11次維修服務?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一條小河岸邊有相距![]() 的
的![]() 兩個村莊(村莊視為岸邊上
兩個村莊(村莊視為岸邊上![]() 兩點),在小河另一側有一集鎮
兩點),在小河另一側有一集鎮![]() (集鎮視為點
(集鎮視為點![]() ),
),![]() 到岸邊的距離
到岸邊的距離![]() 為
為![]() ,河寬
,河寬![]() 為
為![]() ,通過測量可知,
,通過測量可知,![]() 與
與![]() 的正切值之比為
的正切值之比為![]() .當地政府為方便村民出行,擬在小河上建一座橋
.當地政府為方便村民出行,擬在小河上建一座橋![]() (
(![]() 分別為兩岸上的點,且
分別為兩岸上的點,且![]() 垂直河岸,
垂直河岸,![]() 在
在![]() 的左側),建橋要求:兩村所有人到集鎮所走距離之和最短,已知
的左側),建橋要求:兩村所有人到集鎮所走距離之和最短,已知![]() 兩村的人口數分別是
兩村的人口數分別是![]() 人、
人、![]() 人,假設一年中每人去集鎮的次數均為
人,假設一年中每人去集鎮的次數均為![]() 次.設
次.設![]() .(小河河岸視為兩條平行直線)
.(小河河岸視為兩條平行直線)

(1)記![]() 為一年中兩村所有人到集鎮所走距離之和,試用
為一年中兩村所有人到集鎮所走距離之和,試用![]() 表示
表示![]() ;
;
(2)試確定![]() 的余弦值,使得
的余弦值,使得![]() 最小,從而符合建橋要求.
最小,從而符合建橋要求.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的健身方式,小明的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的40人(男、女各20人),記錄了他們某一天的走路步數,并將數據整理如下:
| 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 |
|
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)若采用樣本估計總體的方式,試估計小明的所有微信好友中每日走路步數超過5000步的概率;
(2)已知某人一天的走路步數超過8000步時被系統評定為“積極型”,否則為“懈怠型”.根據小明的統計完成下面的![]() 列聯表,并據此判斷是否有
列聯表,并據此判斷是否有![]() 以上的把握認為“評定類型”與“性別”有關?
以上的把握認為“評定類型”與“性別”有關?
積極型 | 懈怠型 | 總計 | |
男 | |||
女 | |||
總計 |
附:![]()
![]()
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象在
的圖象在![]() 軸右側的第一個最高點和第一個最低點的坐標分別為
軸右側的第一個最高點和第一個最低點的坐標分別為![]() 和
和![]() .若將函數
.若將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度后得到的圖象關于原點對稱.
個單位長度后得到的圖象關于原點對稱.
(1)求函數![]() 的解析式;
的解析式;
(2)若函數![]() 的周期為
的周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com